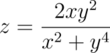Difference between revisions of "Documentation:Tutorial Section 3.2"
Jholsenback (talk | contribs) m (continued isosurface cleanup and formatting) |
Jholsenback (talk | contribs) m (continued cleanup) |
||
| Line 213: | Line 213: | ||
=====Specifying functions===== | =====Specifying functions===== | ||
| − | <p> | + | <p>Until now, we have seen, the functions used to define the isosurface were literally written in the <code>function {...}</code> block:</p> |
| + | <pre> | ||
| + | #declare Threshold = 1; | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
isosurface { | isosurface { | ||
function {pow(x,2) + pow(y,2) + pow(z,2)} | function {pow(x,2) + pow(y,2) + pow(z,2)} | ||
| Line 228: | Line 224: | ||
</pre> | </pre> | ||
| − | <p> | + | <p>Let's expand on that concept, and add some flexibility. Remember that user defined functions (like equations), all float expressions and operators which are legal in POV-Ray can be used, and that functions should be declared first, and then used in the isosurface. See the section <!--<linkto "User-Defined Functions">User-Defined Functions</linkto>--->[[Documentation:Reference Section 2.2#User-Defined Functions|User-Defined Functions]] for more information.</p> |
| − | + | ||
| + | <p>This next example takes the above equation, and rewrites it as a user defined function. By default a function that takes three parameters (x,y,z) does not require you to explicitly specify the parameter names when declaring it, however when <em>using</em> the identifier, the parameters <em>must</em> be specified.</p> | ||
| + | |||
<pre> | <pre> | ||
| − | #declare Sphere = function {pow(x,2) + pow(y,2) + pow(z,2)} | + | #declare Threshold = 1; |
| + | |||
| + | #declare Sphere = function {pow(x,2) + pow(y,2) + pow(z,2)}; | ||
| + | |||
isosurface { | isosurface { | ||
function { Sphere(x,y,z) } | function { Sphere(x,y,z) } | ||
| Line 239: | Line 240: | ||
</pre> | </pre> | ||
| − | <p> | + | <p>However, if you need more or less than three parameters when declaring a function, you will also have to explicitly specify the parameter names.</p> |
| − | |||
| − | |||
| − | |||
| − | to explicitly specify the parameter names.</p> | ||
<pre> | <pre> | ||
| − | #declare Sphere = function(x,y,z,Radius) { | + | #declare Sphere = function (x,y,z,Radius) {pow(x,2) + pow(y,2) + pow(z,2) - pow(Radius,2)}; |
| − | + | ||
| − | |||
isosurface { | isosurface { | ||
function { Sphere(x,y,z,1) } | function { Sphere(x,y,z,1) } | ||
Revision as of 10:25, 15 April 2011
|
This document is protected, so submissions, corrections and discussions should be held on this documents talk page. |
Isosurface Object
Simple functions
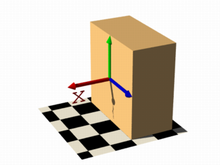
Let's begin with something simple. In this first series of images, let's explore the user defined function shown as function { x } that we see in the code example below. It produces the first image on the left, a simple box. The container, which is a requirement for the isosurface object, is represented by the box object and the contained_by keyword in the isosurface definition.
isosurface {
function { x }
contained_by { box { -2, 2 } }
}
You should have also noticed that in the image on the left, only half the box was produced, that's because the threshold keyword was omitted, so the default value 0 was used to evaluate the x-coordinate.
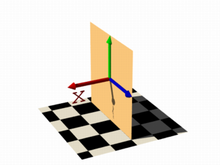
In this next code example threshold 1 was added to produce the center image.
isosurface {
function { x }
threshold 1
contained_by { box { -2, 2 } }
}
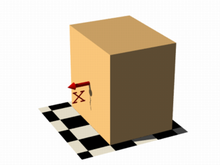
It is also possible to remove the visible surfaces of the container by adding the open keyword to the isosurface definition.
For the final image on the right, the following code example was used. Notice that the omission of the threshold keyword causes the x-coordinate to be again evaluated to zero.
isosurface {
function { x }
open
contained_by { box { -2, 2 } }
}
|
function { x } |
function { x } with threshold 1 |
function { x } with open |
Hint: The checkered ground plane is scaled to one unit squares.
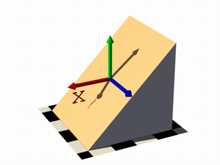
For the last series of images in this section, let's try something different. These next two code examples were used to show the results of changing the user defined function to function { x+y } and function { x+y+z } respectively. They describe planes going through the origin, the function just describes the normal vector of the plane.
isosurface {
function { x+y }
max_gradient 4
contained_by { box { -2, 2 } }
}
Note: To properly render these examples max_gradient 4 was added to the isosurface definition, and will be explained later.
isosurface {
function { x+y+z }
max_gradient 4
contained_by { box { -2, 2 } }
}
|
plane function { x+y } |
plane function { x+y+z } |
Note: When appropriate, to better visualize the difference between the isosurface and the container object, the images in this tutorial have been color coded.
Several surfaces
Now that you're starting to become familiar with isosurface syntax, there really isn't any need to show a code example for each and every image. You can always look back at the earlier examples when needed. The image captions will most often contain additional keyword hints when appropriate.
Note: The user defined function portion will always use this color coded format: function { x+y+z }
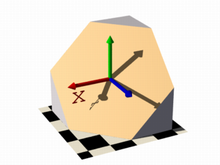
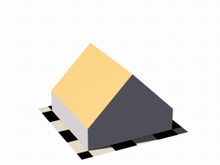
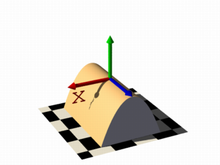
For the first image on the left, these two functions lead to identical results: function { abs(x)-1 } and function { sqrt(x*x)-1 } because both of these formulas have the same solution where the function value is 0, specifically x=-1 and x=1 in this example.
You can easily mix any of these elements in different combinations, but the results always produce planar surfaces. The last two images in this series used function { abs(x)-1+y } and function { abs(x)+abs(y)+abs(z)-2 } respectively.
|
identical results with open |
linear functions x & y axis |
linear functions x, y & z axis |
Non-linear functions
|
Curved surfaces of many different kinds can be achieved with non-linear
functions. A square function creates the parabolic shape: |
|
|
a parabolic shape |
|
If you describe a circle in 2 dimensions with a constant in the 3rd dimension you get a cylinder: |
|
|
the cylinder shape |
|
It's easy to change a cylinder into a cone, we just need
to add a linear component in y-direction: |
||
|
the cone shape |
|
No worries, creating a sphere is easy too. In this example |
|
|
the sphere shape |
Specifying functions
Until now, we have seen, the functions used to define the isosurface were literally written in the function {...} block:
#declare Threshold = 1;
isosurface {
function {pow(x,2) + pow(y,2) + pow(z,2)}
threshold Threshold
...
}
Let's expand on that concept, and add some flexibility. Remember that user defined functions (like equations), all float expressions and operators which are legal in POV-Ray can be used, and that functions should be declared first, and then used in the isosurface. See the section User-Defined Functions for more information.
This next example takes the above equation, and rewrites it as a user defined function. By default a function that takes three parameters (x,y,z) does not require you to explicitly specify the parameter names when declaring it, however when using the identifier, the parameters must be specified.
#declare Threshold = 1;
#declare Sphere = function {pow(x,2) + pow(y,2) + pow(z,2)};
isosurface {
function { Sphere(x,y,z) }
threshold Threshold
...
}
However, if you need more or less than three parameters when declaring a function, you will also have to explicitly specify the parameter names.
#declare Sphere = function (x,y,z,Radius) {pow(x,2) + pow(y,2) + pow(z,2) - pow(Radius,2)};
isosurface {
function { Sphere(x,y,z,1) }
...
}
Internal functions
There are a lot of internal functions available in POV-Ray. For example
a sphere could also be generated with function { f_sphere(x, y, z, 2) }
These functions are declared in the functions.inc include file.
Most of them are more complicated and it is usually faster to use them instead of a
hand coded equivalent. See the
complete list for details.
The following makes a torus just like POV-Ray's torus object:
#include "functions.inc"
isosurface {
function { f_torus(x, y, z, 1.6, 0.4) }
contained_by { box { -2, 2 } }
}
|
Isosurface sample (torus function) |
The 4th and 5th parameter are the major and minor radius,
just like the corresponding values in the torus{} object.
The parameters x, y and z are required, because it is a declared function. You can also declare functions yourself like it is explained in the reference section.
Combining isosurface functions
We can also simulate some Constructive Solid Geometry with isosurface functions. If you do not know about CSG we suggest you have a look at "What is CSG?" or the corresponding part of the reference section first.
We will take two functions: a cylinder and a rotated box:
#declare fn_A = function { sqrt(pow(y,2) + pow(z,2)) - 0.8 }
#declare fn_B = function { abs(x)+abs(y)-1 }
If we combine them the following way, we get a merge:
function { min(fn_A(x, y, z), fn_B(x, y, z)) }
|
Isosurface sample (merge) |
An intersection can be obtained by using
max() instead of min():
function { max(fn_A(x, y, z), fn_B(x, y, z)) }
|
Isosurface sample (intersection) |
Of course also difference is possible, we just have to add a minus (-) before the second function:
function { max(fn_A(x, y, z), -fn_B(x, y, z)) }
|
Isosurface sample (difference) |
Apart from basic CSG you can also obtain smooth transits between the different surfaces (like with the blob object)
#declare Blob_threshold=0.01;
isosurface {
function {
(1+Blob_threshold)
-pow(Blob_threshold, fn_A(x,y,z))
-pow(Blob_threshold, fn_B(x,y,z))
}
max_gradient 4
contained_by { box { -2, 2 } }
}
|
Isosurface sample (blob) |
The Blob_threshold value influences the smoothness of
the transit between the shapes. a lower value leads to sharper edges.
The function for a negative blob looks like:
function{fn_A(x,y,z) + pow(Blob_threshold,(Fn_B(x,y,z) + Strength))}
Noise and pigment functions
Some of the internal functions have a random or noise-like structure
Together with the pigment functions they are one of the most powerful tools for designing isosurfaces. We can add real surface displacement to the objects rather than only normal perturbation known from the normal statement.
The relevant internal functions are:
f_noise3d(x,y,z)
uses the noise generator specified inglobal_settings{}and generates structures like the bozo pattern.f_noise_generator(x, y, z, noise_generator)
generates noise with a specified noise generator.f_ridged_mf(x, y, z, H, Lacunarity, Octaves, Offset, Gain, noise_generator)
generates a ridged multifractal pattern.f_ridge(x, y, z, Lambda, Octaves, Omega, Offset, Ridge, noise_generator)
generates another noise with ridges.f_hetero_mf(x, y, z, H, Lacunarity, Octaves, Offset, T, noise_generator)
generates heterogenic multifractal noise.
Using pure noise3d as a function results in the following picture:
function { f_noise3d(x, y, z)-0.5 }
|
Isosurface sample (noise3d) |
Note: The -0.5 is only there to make it match to the used threshold value of 0, the f_noise3d function returns values between 0 and 1.
With this and the other functions you can generate objects similar to heightfields, having the advantage that a high resolution can be achieved without high memory requirements.
function { x + f_noise3d(0, y, z) }
|
Isosurface sample (noise3d - heightfield) |
The noise function can of course also be subtracted which results in an 'inverted' version:
function { x - f_noise3d(0, y, z) }
|
Isosurface sample (noise3d - heightfield inverted) |
In the last two pictures we added the noise function to a plane function. The x-parameter was set to 0 so the noise function is constant in x-direction. This way we achieve the typical heightfield structure.
Of course we can also add noise to any other function. If the noise function is very strong this can result in several separated surfaces.
function { f_sphere(x, y, z, 1.2) - f_noise3d(x, y, z) }
|
Isosurface sample (noise3d on a sphere) |
This is a noise function applied to a sphere surface, we can influence the intensity of the noise by multiplying it with a factor and change the scale by multiplying the coordinate parameters:
function { f_sphere(x, y, z, 1.6) - f_noise3d(x * 5, y * 5, z * 5) * 0.5 }
|
Isosurface sample (noise3d on a sphere scaled) |
As alternative to noise functions we can also use any pigment in a function:
#declare fn_Pigm=function {
pigment {
agate
color_map {
[0 color rgb 0]
[1 color rgb 1]
}
}
}
This function is a vector function returning a (color) vector.For use in isosurface functions they must be declared first. When using the identifier, you have to specify which component of the color vector should be used. To do this, the dot notation is used: Function(x,y,z).red.
A color vector has five components. Supported dot types to access these components are:
-
F( ).
x| F( ).u| F( ).red- to get the red value of the color vector
-
F( ).
y| F( ).v| F( ).green- to get the green value of the color vector
-
F( ).
z| F( ).blue- to get the blue value of the color vector
-
F( ).
filter| F( ).t- to get the filter value of the color vector
-
F( ).
transmit- to get the transmit value of the color vector
-
F( ).
gray- to get the gray value of the color vector
- gray value = Red*29.7% + Green*58.9% + Blue*11.4%
-
F( ).
hf- to get the height_field value of the color vector
- hf value = (Red + Green/255)*0.996093
- the .hf operator is experimental and will generate a warning.
function { f_sphere(x, y, z, 1.6)-fn_Pigm(x/2, y/2, z/2).gray*0.5 }
|
Isosurface sample (pigment function) |
There are quite a lot of things possible with pigment functions, but you probably have recognized that this renders quite slow.
Conditional directives and loops
Conditional directives are allowed in functions:
#declare Rough = yes;
#include "functions.inc"
isosurface {
function { y #if(Rough=1)-f_noise3d(x/0.5,y/0.3,z/0.4)*0.8 #end }
...
}
Loops can also be used in functions:
#include "functions.inc"
#declare Thr = 1/1000;
#declare Ang = radians(45);
#declare Offset = 1.5;
#declare Scale = 1.2;
#declare TrSph = function { f_sphere(x-Offset,y,z,0.7*Scale) }
function {
(1-Thr)
#declare A = 0;
#while (A<8)
-pow(Thr, TrSph(x*cos(A*Ang) + y*sin(A*Ang),
y*cos(A*Ang) -x*sin(A*Ang), z) )
#declare A=A+1;
#end
}
Note: The loops and conditionals are evaluated at parse time, not at render time.
Transformations on functions
Transforming an isosurface object is done like transforming any POV-Ray object. Simply use the object modifiers (scale, translate, and rotate).
However, when you want to transform functions within the contained_by object, you have to substitute parameters in the functions.
The results seem inverted to what you would normally expect. Here is an explanation:
Take a
Sphere(x,y,z). We know it sits at the origin because x=0. When we want it at x=2 (translating 2 units to the right) we
need to write the second equation in the same form: x-2=0
Now that both equations equal 0, we can replace
parameter x with x-2
So our Sphere(x-2, y,z) moves two units to the right.
Let's scale our Sphere 0.5 in the y direction. Default size is y=1 (one unit). We want y=0.5.
To get this
equation in the same form as the first one, we have to multiply both sides by two. y*2 = 0.5*2, which gives y*2=1
Now
we can replace the y parameter in our sphere: Sphere(x, y*2, z). This squishes the y-size of the sphere by half.
Well,
this is the general idea of substitutions.
Here is an overview of some useful substitutions:
Using a declared object P(x,y,z)
Scale
scale x : replace "x" with "x/scale" (idem other parameters)
scale x*2 gives P(x/2,y,z)
Scale Infinitely
scale x infinitely : replace "x" with "0" (idem other parameters)
scale y infinitely gives P(x,0,z)
Translate
translate x : replace "x" with "x - translation" (idem other
parameters)
translate z*3 gives P(x,y,z-3)
Shear
shear in XY-plane : replace "x" with "x + y*tan(radians(Angle))"
(idem other parameters)
shear 45 degrees left gives P(x+y*tan(radians(45)), y, z)
Rotate
Note: These rotation substitutions work like normal POV-rotations: they already compensate for the inverse working
rotate around X
: replace "y" with "z*sin(radians(Angle)) +
y*cos(radians(Angle))"
: replace "z" with "z*cos(radians(Angle)) -
y*sin(radians(Angle))"
rotate around Y
: replace "x" with "x*cos(radians(Angle)) -
z*sin(radians(Angle))"
: replace "z" with "x*sin(radians(Angle)) +
z*cos(radians(Angle))"
rotate around Z
: replace "x" with "x*cos(radians(Angle)) +
y*sin(radians(Angle))"
: replace "y" with "-x*sin(radians(Angle)) +
y*cos(radians(Angle)) "
rotate z*75 gives:
P(x*cos(radians(75)) + y*sin(radians(75)),
-x*sin(radians(75)) + y*cos(radians(75)), z)
Flip
flip X - Y : replace "x" with "y" and replace "y"
with "-x"
flip Y - Z : replace "y" with "z" and replace "z"
with "-y"
flip X - Z : replace "x" with "-z" and replace "z"
with "x"
flip x and y gives P(y, -x, z)
Twist
twist N turns/unit around X
: replace "y" with "z*sin(x*2*pi*N)
+ y*cos(x*2*pi*N)"
: replace "z" with "z*cos(x*2*pi*N) -
y*sin(x*2*pi*N)"
Improving Isosurface Speed
To optimize the approximation of the isosurface and to get maximum rendering speed it is important to adapt certain values;
accuracy
The accuracy value influences how accurate the surface geometry is calculated.
Lower values lead to a more precise, but slower result.
The default value of 0.001 is fairly low. We used this value in all the
previous samples, but often you can raise this quite a
lot and thereby make things faster.
max_gradient
For finding the actual surface it is important for POV-Ray to know the
maximum gradient of the function, meaning how fast the function value changes.
We can specify a value with the max_gradient keyword. Lower
max_gradient values lead to faster rendering, but if the specified value is
below the actual maximum gradient of the function, there can be holes or
other artefacts in the surface.
For the same reason functions with infinite gradient should not be used.
This applies for pigment functions with brick or checker pattern for example.
You should also be careful when using select() in isosurface
functions because of this.
If the real maximum gradient differs too much from the specified value
POV-Ray prints a warning together with the found maximum gradient.
It is usually sufficient to use this number for the max_gradient
parameter to get fast and correct results.
POV-Ray can also dynamically change the max_gradient when you
specify evaluate with 3 parameters the isosurface definition.
Concerning the details on this and other things see the
evaluate in the reference section.
contained_by
Make sure your contained_by 'object' fits as tightly as possible. An oversized container can
sky-rocket the render time.
When the container has a lot of empty space around the actual isosurface, POV-Ray has
to do a lot of superfluous sampling: especially with complex functions this can become very time consuming. On top of
this, the max_gradient needed to get a proper surface will also increase rapidly (almost proportional to
the oversize!).
You could use a transparent copy of the container (using exactly the same transformations) to
check how it fits. Getting the min_extent and max_extent of the isosurface
is not useful because it only gives the extent of the container and not of the actual isosurface.
Poly Object
The polynomial object (and its shortcut versions: cubic, quartic and quadric)
of POV-Ray is one of the most complex and
mathematical primitives of the program. One could think that it is seldom
used and more or less obsolete, but we have to remember that for example
the torus primitive is just a shortcut for the equivalent quartic, which
is just a shortcut for the equivalent poly object. Polys are, however, seldom
used in scenes due to the fact that they are so difficult to define and
it is far from trivial to get the desired shape with just a polynomial
equation. It is mostly used by the most mathematically oriented POV-Ray
users.
This tutorial explains the process of making a polynomial object in POV-Ray.
Note: Since version 3.5, POV-Ray includes the new isosurface object
which makes the polynomial object more or less obsolete. The isosurface is more versatile (you can specify any mathematical function, not
just polynomials) and easier to use. You can write the function as is, without needing to put values in a gigantic vector. Isosurfaces also often (although not always) render considerably faster than equivalent polys.
However, the most mathematically oriented still like polys because isosurfaces are calculated just by approximating the right value, while the poly is calculated in a mathematically exact way. Usually isosurfaces are more than good enough for most applications, though.
Note: A maximum of 35th degree polynomial can be represented with the poly object. If a higher degree polynomial or other non-polynomial function has to be represented, then it is necessary to use the isosurface object.
Creating the polynomial function
The first step is to create the polynomial function to be represented. You will need some (high-school level) mathematical knowledge for this.
1) Let's start with an easy example, a sphere:
The sphere function is:
|
sphere function |
Now we have to convert this to polynomial form, we will need a polynomial of the 2nd degree to represent this:
|
sphere polynomial |
2) A more elaborated example:
Let's take the function:
|
function |
Converting this to polynomial form we get:
|
polynomial |
Although the highest power is 4 we will need a 5th order polynomial to represent this function (because we cannot represent y4z with a 4th order polynomial).
3) And since we talked about the torus, let's also take it as an example.
A torus can be represented with the function:
|
torus function |
where r1 is the major radius and r2 is the minor radius.
Now, this is tougher to convert to polynomial form, but finally we get:
|
torus polynomial |
A 4th order polynomial is enough to represent this.
Note: Not every function can be represented in polynomial form. Only functions that use addition (and substraction), multiplication (and division) and scalar powers (including rational powers, eg. the square root) can be represented. Also, the poly primitive supports only polynomials of the 35th degree at max.
Converting a function to polynomial form may be a very laborious task for certain functions. Some mathematical programs are very helpful in this matter.
Writing the polynomial vector
Now that we have the function in polynomial form, we have to write it in POV-Ray syntax. The syntax is specified in the in the chapters Poly, Cubic and Quartic and Quadric of the reference section. There is also a table in this chapter which we will be using to make the polynomial vector. It is easier to have this table printed on paper.
Note: It is also possible to make a little program with your favorite programming language which will print the poly vector from the polynomial function, but making a program like this is up to you.
1) Let's start with the easy one, ie. the sphere.
Since the sphere can be represented with a polynomial of 2nd degree, we look at the column titled 2nd in the table. We see that it has 10 items, ie. we need a vector of size 10. Each item of the vector will be the factor of the term listed in the table.
The polynomial was:
|
sphere polynomial function |
Writing the poly in this way we get:
#declare Radius=1;
poly
{ 2,
<1,0,0,0,1,
0,0,1,0,-Radius*Radius>
}
Put each group of factors (separated with lines in the table) in their own lines.
In the table we see that the first item is the factor for x2, which is 1 in the function. The next item is xy. Since it is not in the function, its factor is 0. Likewise the next item, which is xz. And so on. The last item is the scalar term, which is in this case -r2.
If we make a proper scene and render it, we get:
camera { location y*4-z*5 look_at 0 angle 35 }
light_source { <100,200,-50> 1 }
background { rgb <0,.25,.5> }
#declare Radius=1;
poly
{ 2,
<1,0,0,0,1,
0,0,1,0,-Radius*Radius>
pigment { rgb <1,.7,.3> } finish { specular .5 }
}
|
sphere polynomial image |
Note: There is a shortcut for 2nd degree polynomials: The
quadric
primitive. Using a shortcut version, whenever possible, can lead to faster
renderings. We can write the sphere code described above in the following
way:
quadric
{ <1,1,1>, <0,0,0>, <0,0,0>, -Radius*Radius
pigment { rgb <1,.7,.3> } finish { specular .5 }
}
2) Now lets try the second one. We do it similarly, but this time we need to look at the column titled 5th in the table.
The polynomial was:
|
5th order polynomial function |
Writing the poly primitive we get:
poly
{ 5,
<0,0,0,0,0,
0,0,0,0,0,
0,0,0,0,0,
0,0,0,1,0,
0,0,0,0,0,
-2,0,0,0,0,
0,0,0,0,0,
0,1,0,0,0,
0,0,0,0,0,
0,0,0,0,0,
0,0,0,0,0,0>
}
With the proper scene we get:
camera { location <8,20,-10>*.7 look_at x*.01 angle 35 }
light_source { <100,200,20> 1 }
background { rgb <0,.25,.5> }
poly
{ 5,
<0,0,0,0,0,
0,0,0,0,0,
0,0,0,0,0,
0,0,0,1,0,
0,0,0,0,0,
-2,0,0,0,0,
0,0,0,0,0,
0,1,0,0,0,
0,0,0,0,0,
0,0,0,0,0,
0,0,0,0,0,0>
clipped_by { box { <-4,-4,-1><4,4,1> } }
bounded_by { clipped_by }
pigment { rgb <1,.7,.3> } finish { specular .5 }
rotate <0,90,-90>
}
|
5th order polynomial image |
3) And finally the torus:
The polynomial was:
|
torus polynomial function |
And we get the proper 4th degree poly primitive:
camera { location y*4-z*5 look_at 0 angle 35 }
light_source { <100,200,-50> 1 }
background { rgb <0,.25,.5> }
#declare r1=1;
#declare r2=.5;
poly
{ 4,
<1,0,0,0,2,
0,0,2,0,-2*(r1*r1+r2*r2),
0,0,0,0,0,
0,0,0,0,0,
1,0,0,2,0,
2*(r1*r1-r2*r2),0,0,0,0,
1,0,-2*(r1*r1+r2*r2),0,pow(r1,4)+pow(r2,4)-2*r1*r1*r2*r2>
pigment { rgb <1,.7,.3> } finish { specular .5 }
}
When rendered we get:
|
torus polynomial image |
There is a shortcut for 4th order polynomials: The
quartic primitive.
We can write the torus like this:
quartic
{ <1,0,0,0,2,
0,0,2,0,-2*(r1*r1+r2*r2),
0,0,0,0,0,
0,0,0,0,0,
1,0,0,2,0,
2*(r1*r1-r2*r2),0,0,0,0,
1,0,-2*(r1*r1+r2*r2),0,pow(r1,4)+pow(r2,4)-2*r1*r1*r2*r2>
pigment { rgb <1,.7,.3> } finish { specular .5 }
}
Polynomial made easy
Since consulting the table in the section Poly, Cubic and Quartic or writing a program to get the right poly vector can be a bit cumbersome, especially when the poly vector is not a write-once-only expression and that you want to get it back, so let's examine how those equations would be rewritten using the simplified syntax.
You should refer to the images in the previous section, as these examples produce exactly the same results.
1) The sphere example can be rewritten as:
#declare Radius=1;
polynomial { 2,
xyz(2,0,0):1,
xyz(0,2,0):1,
xyz(0,0,2):1,
xyz(0,0,0):-Radius*Radius
}
2) Let's now see the second one:
polynomial { 5,
xyz(2,0,1):1,
xyz(0,4,1):1,
xyz(1,2,0):-2
}
3) And finally the torus example:
polynomial { 4,
xyz(4,0,0):1,
xyz(2,2,0):2,
xyz(2,0,2):2,
xyz(2,0,0):-2*(r1*r1+r2*r2),
xyz(0,4,0):1,
xyz(0,2,2):2,
xyz(0,2,0):2*(r1*r1-r2*r2),
xyz(0,0,4):1,
xyz(0,0,2):-2*(r1*r1+r2*r2),
xyz(0,0,0):pow((r1*r1-r2*r2),2)
}
| Isosurface Object | Superquadric Ellipsoid Object |
|
This document is protected, so submissions, corrections and discussions should be held on this documents talk page. |