Difference between revisions of "Reference:Ovus"
Jholsenback (talk | contribs) m (1 revision: Reference Migration Initial Load) |
Jholsenback (talk | contribs) m (added precision default) |
||
| (7 intermediate revisions by 2 users not shown) | |||
| Line 3: | Line 3: | ||
{{#indexentry:ovus, keyword}} | {{#indexentry:ovus, keyword}} | ||
{{#indexentry:keyword, ovus}} | {{#indexentry:keyword, ovus}} | ||
| − | <p>An <code>ovus</code> is a shape that looks like an egg. | + | <p>An <code>ovus</code> is a shape that looks like an egg. A {{Change}} in version 3.8 has extended the syntax of the <code>ovus</code> object by adding <code>radius</code>, <code>distance</code> and <code>precision</code> controls.</p> |
| + | <p>The syntax is as follows:</p> | ||
<pre> | <pre> | ||
| − | + | ovus { | |
| − | + | Bottom_radius, Top_radius [radius Inner_radius] [distance Vertical_distance] [precision Root_tolerance] | |
| − | + | [OBJECT_MODIFIERS...] | |
| − | + | } | |
| − | |||
</pre> | </pre> | ||
| + | |||
| + | <p>Where <em>Bottom_radius</em> is a float value giving the radius of the bottom sphere and <em>Top_radius</em> is a float specifying the radius of the top sphere. The top and bottom spheres are connected together with a suitably truncated lemon, or self intersection of a torus, that is automatically computed so as to provide the needed continuity to the shape. The <code>distance</code> is a float value that represents the length between the center of the two spheres, defaulting to <em>Bottom_radius</em>. The <code>radius</code> float value represents the inner circle of the connecting torus and it's default is twice the greater of either <em>Top_radius</em> or <em>Bottom_radius</em>. The <code>precision</code> float value is the tolerance used for the root solving of the connecting torus, and it's default is <code>1e-4</code>. If additional accuracy is required you can now add the <code>[[Reference:Sturm Object Modifier|sturm]]</code> object modifier.</p> | ||
<table class="centered" width="700px" cellpadding="0" cellspacing="10"> | <table class="centered" width="700px" cellpadding="0" cellspacing="10"> | ||
<tr> | <tr> | ||
| − | |||
| − | |||
| − | |||
<td>[[Image:RefImgOvus2D.png|center|125px<!--left--->]]</td> | <td>[[Image:RefImgOvus2D.png|center|125px<!--left--->]]</td> | ||
<td> | <td> | ||
<ul> | <ul> | ||
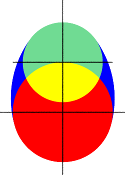
| − | <li>The center of the top sphere lies on the top of the bottom sphere | + | <li>The center of the top sphere lies on the top of the bottom sphere</li> |
| − | <li>The bottom sphere of the <code>ovus</code> is centered at the origin | + | <li>The bottom sphere of the <code>ovus</code> is centered at the origin</li> |
| − | <li>The top sphere of the <code>ovus</code> lies on the y-axis | + | <li>The top sphere of the <code>ovus</code> lies on the y-axis</li> |
| + | <li>The minor radius of the lemon is twice the largest radius</li> | ||
| + | <li>The <code>distance</code> <em>must</em> be greater than or equal to <em>Bottom_radius</em></li> | ||
| + | <li>The <code>radius</code> <em>must</em> be greater than or equal to half the sum of <em>Bottom_radius</em>, <em>Top_radius</em> and <em>Vertical_distance</em></li> | ||
</ul> | </ul> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
| − | + | <td><p class="caption">An ovus 2D section</p></td> | |
| − | |||
<td></td> | <td></td> | ||
</tr> | </tr> | ||
| Line 41: | Line 42: | ||
</tr> | </tr> | ||
</table> | </table> | ||
| − | |||
| − | |||
<p class="Note"><strong>Note:</strong> According to the ratio of the radius, the pointy part is the smallest radius, but is <em>not</em> always on top!</p> | <p class="Note"><strong>Note:</strong> According to the ratio of the radius, the pointy part is the smallest radius, but is <em>not</em> always on top!</p> | ||
| Line 54: | Line 53: | ||
</tr> | </tr> | ||
</table> | </table> | ||
| + | |||
| + | <p>See also: [[Reference:UV Mapping#Supported Objects|UV Mapping]].</p> | ||
<p class="Note"><strong>Note:</strong> See the following <em>MathWorld</em> references for more information about the math behind how the <code>ovus</code> object is constructed.</p> | <p class="Note"><strong>Note:</strong> See the following <em>MathWorld</em> references for more information about the math behind how the <code>ovus</code> object is constructed.</p> | ||
Latest revision as of 11:07, 25 July 2017
An ovus is a shape that looks like an egg. A Change in version 3.8 has extended the syntax of the ovus object by adding radius, distance and precision controls.
The syntax is as follows:
ovus {
Bottom_radius, Top_radius [radius Inner_radius] [distance Vertical_distance] [precision Root_tolerance]
[OBJECT_MODIFIERS...]
}
Where Bottom_radius is a float value giving the radius of the bottom sphere and Top_radius is a float specifying the radius of the top sphere. The top and bottom spheres are connected together with a suitably truncated lemon, or self intersection of a torus, that is automatically computed so as to provide the needed continuity to the shape. The distance is a float value that represents the length between the center of the two spheres, defaulting to Bottom_radius. The radius float value represents the inner circle of the connecting torus and it's default is twice the greater of either Top_radius or Bottom_radius. The precision float value is the tolerance used for the root solving of the connecting torus, and it's default is 1e-4. If additional accuracy is required you can now add the sturm object modifier.
|
|
An ovus 2D section |
The ovus and it's constituent 3D shapes |
Note: According to the ratio of the radius, the pointy part is the smallest radius, but is not always on top!
Evolution of ratio from 0 to 1.95 in 0.15 steps. |
See also: UV Mapping.
Note: See the following MathWorld references for more information about the math behind how the ovus object is constructed.