Difference between revisions of "Reference:Torus"
(added spindle torus section) |
Jholsenback (talk | contribs) m (version changes) |
||
| (5 intermediate revisions by 2 users not shown) | |||
| Line 3: | Line 3: | ||
{{#indexentry:torus, keyword}} | {{#indexentry:torus, keyword}} | ||
{{#indexentry:keyword, torus}} | {{#indexentry:keyword, torus}} | ||
| − | <p>A <code>torus</code> is a 4th order quartic polynomial shape that looks | + | <p>A <code>torus</code> is a 4th order quartic polynomial shape that looks like a donut or inner tube. Because this shape is so useful and quartics are difficult to define, POV-Ray lets you take a short-cut and define a torus by:</p> |
| − | like a donut or inner tube. Because this shape is so useful and quartics are | ||
| − | difficult to define, POV-Ray lets you take a short-cut and define a torus | ||
| − | by:</p> | ||
<pre> | <pre> | ||
TORUS: | TORUS: | ||
| Line 26: | Line 23: | ||
</pre> | </pre> | ||
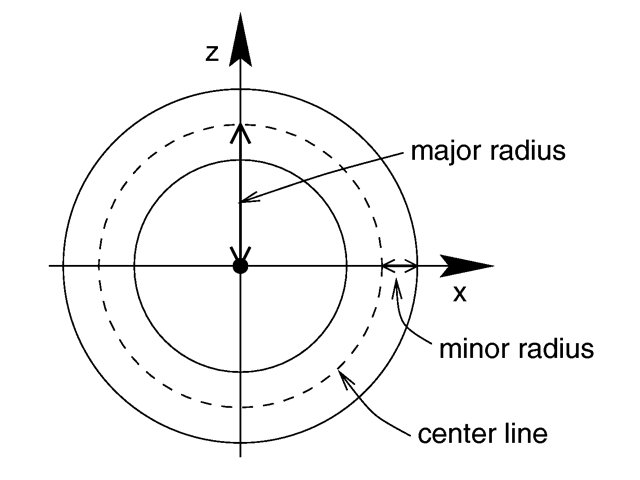
| − | <p>where <em><code>Major</code></em> is a float value giving the major radius | + | <p>where <em><code>Major</code></em> is a float value giving the major radius and <em><code>Minor</code></em> is a float specifying the minor radius. The major radius extends from the center of the hole to the mid-line of the rim while the minor radius is the radius of the cross-section of the rim. The torus is centered at the origin and lies in the x-z-plane with the y-axis |
| − | and <em><code>Minor</code></em> is a float specifying the minor radius. The | ||
| − | major radius extends from the center of the hole to the mid-line of the rim | ||
| − | while the minor radius is the radius of the cross-section of the rim. The | ||
| − | torus is centered at the origin and lies in the x-z-plane with the y-axis | ||
sticking through the hole.</p> | sticking through the hole.</p> | ||
| Line 46: | Line 39: | ||
</table> | </table> | ||
| − | <p>The torus is internally bounded by two cylinders and two rings forming a | + | <p>The torus is internally bounded by two cylinders and two rings forming a thick cylinder. With this bounding cylinder the performance of the torus intersection test is vastly increased. The test for a valid torus intersection, i.e. solving a 4th order polynomial, is only performed if the bounding cylinder is hit. Thus a lot of slow root solving calculations are avoided.</p> |
| − | thick cylinder. With this bounding cylinder the performance of the torus | ||
| − | intersection test is vastly increased. The test for a valid torus | ||
| − | intersection, i.e. solving a 4th order polynomial, is only performed if the | ||
| − | bounding cylinder is hit. Thus a lot of slow root solving calculations are | ||
| − | avoided.</p> | ||
{{#indexentry:keyword, difference, torus}} | {{#indexentry:keyword, difference, torus}} | ||
| Line 57: | Line 45: | ||
{{#indexentry:keyword, merge, torus}} | {{#indexentry:keyword, merge, torus}} | ||
{{#indexentry:keyword, union, torus}} | {{#indexentry:keyword, union, torus}} | ||
| − | + | <p>{{New}} in version 3.8 is a torus with a minor radius greater than the major radius (aka <em>spindle torus</em>) will self-intersect in a spindle-shaped region. The behavior with respect to the spindle can be controlled by specifying either of the <code>difference</code>,<code>intersection</code>, <code>merge</code> or <code>union</code> keywords, which act similar to the corresponding CSG operations:</p> | |
| − | <p>{{New | ||
| − | (aka <em>spindle torus</em>) will self-intersect in a spindle-shaped region. | ||
| − | The | ||
| − | either of the <code>difference</code>, <code>intersection</code>, | ||
| − | <code>merge</code> or <code>union</code> keywords, which act similar to the | ||
| − | corresponding CSG operations:</p> | ||
<ul> | <ul> | ||
| − | <li>Using the <code>difference</code> keyword, the self-intersecting portion | + | <li>Using the <code>difference</code> keyword, the self-intersecting portion is cut away from the torus, so that the spindle volume is considered <em>outside</em> the primitive; the spindle surface is visible (provided you cut open the torus, or make it semi-transparent).</li> |
| − | is cut away from the torus, so that the spindle volume is considered | + | <li>Using the <code>intersection</code> keyword, the resulting shape consists of <em>only</em> the self-intersecting portion, so that only the spindle volume is considered inside the primitive, and only the spindle surface is visible.</li> |
| − | <em>outside</em> the primitive; the spindle surface is visible (provided you | + | <li>Using the <code>merge</code> keyword, the surface within the self-intersecting portion is hidden, so that the spindle surface is <em>not</em> visible; the spindle volume is considered inside the primitive.</li> |
| − | cut open the torus, or make it semi-transparent).</li> | + | <li>Using the <code>union</code> keyword, the entire torus surface remains visible and the spindle volume is considered inside the primitive (this is the default).</li> |
| − | <li>Using the <code>intersection</code> keyword, the resulting shape consists | ||
| − | of <em>only</em> the self-intersecting portion, so that only the spindle volume | ||
| − | is considered inside the primitive, and only the spindle surface is visible.</li> | ||
| − | <li>Using the <code>merge</code> keyword, the surface within the self-intersecting | ||
| − | portion is hidden, so that the spindle surface is <em>not</em> visible; the | ||
| − | spindle volume is considered inside the primitive.</li> | ||
| − | <li>Using the <code>union</code> keyword, the entire torus surface remains | ||
| − | visible and the spindle volume is considered inside the primitive (this is | ||
| − | the default).</li> | ||
</ul> | </ul> | ||
| − | <p>In a non-spindle torus, the <code>intersection</code> keyword will cause a | + | <p>In a non-spindle torus, the <code>intersection</code> keyword will cause a "possible parse error" warning and make the torus invisible, while the other spindle mode keywords will have no effect whatsoever.</p> |
| − | "possible parse error" warning and make the torus invisible, while the other | + | <p class="Note"><strong>Note:</strong> The <code>difference</code> spindle mode does <em>not</em> affect the behavior with respect to the |
| − | spindle mode keywords will have no effect whatsoever.</p> | + | <code>[[Reference:Interior Texture|interior_texture]]</code> keyword. An <code>interior_texture</code> will always be applied to the side of the spindle surface facing the spindle volume.</p> |
| − | <p class="Note"><strong> | ||
| − | does <em>not</em> affect the | ||
| − | <code>[[Reference: | ||
| − | <code>interior_texture</code> will always be applied to the side of the spindle | ||
| − | surface facing the spindle volume.</p> | ||
<table class="centered" width="420px" cellpadding="0" cellspacing="10"> | <table class="centered" width="420px" cellpadding="0" cellspacing="10"> | ||
| Line 102: | Line 70: | ||
{{#indexentry:sturm, torus}} | {{#indexentry:sturm, torus}} | ||
{{#indexentry:keyword, sturm}} | {{#indexentry:keyword, sturm}} | ||
| − | + | ||
| − | <p> | + | <p>If additional accuracy is required you can add the <code>[[Reference:Sturm Object Modifier|sturm]]</code> object modifier.</p> |
| − | |||
| − | |||
Latest revision as of 10:35, 26 June 2017
A torus is a 4th order quartic polynomial shape that looks like a donut or inner tube. Because this shape is so useful and quartics are difficult to define, POV-Ray lets you take a short-cut and define a torus by:
TORUS:
torus {
Major, Minor [SPINDLE_MODE]
[TORUS_MODIFIER...]
}
TORUS_MODIFIER:
sturm | OBJECT_MODIFIER
SPINDLE_MODE:
difference | intersection | merge | union
Torus default values:
union sturm : off
where Major is a float value giving the major radius and Minor is a float specifying the minor radius. The major radius extends from the center of the hole to the mid-line of the rim while the minor radius is the radius of the cross-section of the rim. The torus is centered at the origin and lies in the x-z-plane with the y-axis
sticking through the hole.
|
Major and minor radius of a torus. |
The torus is internally bounded by two cylinders and two rings forming a thick cylinder. With this bounding cylinder the performance of the torus intersection test is vastly increased. The test for a valid torus intersection, i.e. solving a 4th order polynomial, is only performed if the bounding cylinder is hit. Thus a lot of slow root solving calculations are avoided.
New in version 3.8 is a torus with a minor radius greater than the major radius (aka spindle torus) will self-intersect in a spindle-shaped region. The behavior with respect to the spindle can be controlled by specifying either of the difference,intersection, merge or union keywords, which act similar to the corresponding CSG operations:
- Using the
differencekeyword, the self-intersecting portion is cut away from the torus, so that the spindle volume is considered outside the primitive; the spindle surface is visible (provided you cut open the torus, or make it semi-transparent). - Using the
intersectionkeyword, the resulting shape consists of only the self-intersecting portion, so that only the spindle volume is considered inside the primitive, and only the spindle surface is visible. - Using the
mergekeyword, the surface within the self-intersecting portion is hidden, so that the spindle surface is not visible; the spindle volume is considered inside the primitive. - Using the
unionkeyword, the entire torus surface remains visible and the spindle volume is considered inside the primitive (this is the default).
In a non-spindle torus, the intersection keyword will cause a "possible parse error" warning and make the torus invisible, while the other spindle mode keywords will have no effect whatsoever.
Note: The difference spindle mode does not affect the behavior with respect to the
interior_texture keyword. An interior_texture will always be applied to the side of the spindle surface facing the spindle volume.
cutaway view of spindle torus using the |
|||
If additional accuracy is required you can add the sturm object modifier.