Documentation Talk:Reference Section 5.2

• add ovus in the list of supporting shape for UV mapping.

--Le Forgeron 19:24, 2 December 2010 (UTC)

• done: --jholsenback 13:01, 3 December 2010 (UTC)

---

Supported Objects

Surface mapping is currently defined for the following objects:

• bicubic_patch : UV coordinates are based on the patch's parametric coordinates. They stretch with the control points. The default range is (0..1) and can be changed.
   
• mesh, mesh2 : UV coordinates are defined for each vertex and interpolated between.
   
• lathe, sor : modified spherical mapping... the u coordinate (0..1) wraps around the y axis, while the v coordinate is linked to the object's control points (also ranging 0..1).
  Surface of Revolution also has special disc mapping on the end caps if the object is not 'open'.
   
• sphere : boring spherical mapping.
   
• ovus : spherical mapping centered near the center of mass of the ovus (moving from one sphere to another as the ratio of radius progresses).
   
• box : the image is wrapped around the box, as shown below.
   
  
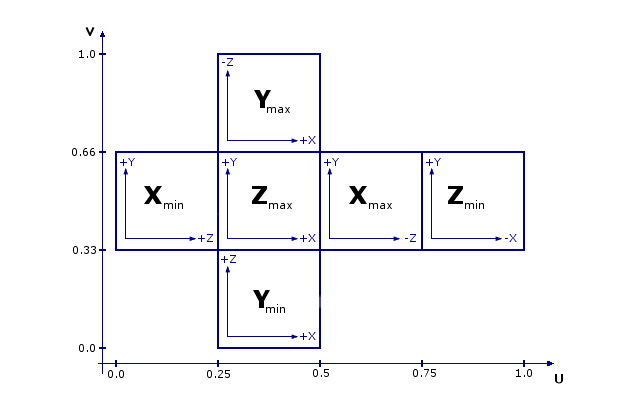
• parametric : In this case the map is not taken from a fixed set of coordinates but the map is taken from the area defined by the boundaries of the uv-space, in which the parametric surface has to be calculated.
   
• torus : The map is taken from the area <0,0><1,1> where the u-coordinate is wrapped around the major radius and the the v-coordinate is wrapped around the minor radius.