Difference between revisions of "Documentation Talk:Reference Section 3"

From POV-Wiki
Jump to navigation Jump to search
m (renamed image to reflect accepted naming convention, and enclosed the image in a table with it's caption)
m (fixed the rest of the images for this section)
Line 1: Line 1:
−
===Handedness===
 
−
<!--<indexentry "Camera, coordinate system" "Coordinate system, camera">--->
 
−
 
−
<p>The <code>right</code> vector also describes the direction to the right of
 
−
the camera. It tells POV-Ray where the right side of your screen is. The sign
 
−
of the <code>right</code> vector can be used to determine the handedness of
 
−
the coordinate system in use. The default value is: <code>
 
−
right&lt;1.33,0,0&gt;</code>. This means that the +x-direction is to the
 
−
right. It is called a <em>left-handed</em> system because you can use your
 
−
left hand to keep track of the axes. Hold out your left hand with your palm
 
−
facing to your right. Stick your thumb up. Point straight ahead with your
 
−
index finger. Point your other fingers to the right. Your bent fingers are
 
−
pointing to the +x-direction. Your thumb now points into +y-direction. Your
 
−
index finger points into the +z-direction.</p>
 
−
<p>
 
−
To use a right-handed coordinate system, as is popular in some CAD programs
 
−
and other ray-tracers, make the same shape using your right hand. Your thumb
 
−
still points up in the +y-direction and your index finger still points
 
−
forward in the +z-direction but your other fingers now say the +x-direction
 
−
is to the left. That means that the right side of your screen is now in the
 
−
-x-direction. To tell POV-Ray to act like this you can use a negative x value
 
−
in the <code> right</code> vector such as: <code>
 
−
right&lt;-1.33,0,0&gt;</code>. Since having x values increasing to the left
 
−
does not make much sense on a 2D screen you now rotate the whole thing 180
 
−
degrees around by using a positive z value in your camera's location. You
 
−
end up with something like this.</p>
 
−
<pre>
 
−
camera {
 
−
  location &lt;0,0,10&gt;
 
−
  up    &lt;0,1,0&gt;
 
−
  right  &lt;-1.33,0,0&gt;
 
−
  look_at &lt;0,0,0&gt;
 
−
  }
 
−
</pre>
 
−
 
−
<p>Now when you do your ray-tracer's aerobics, as explained in the
 
−
section &quot;<!--<linkto "Understanding POV-Ray's Coordinate System">Understanding POV-Ray's Coordinate System</linkto>--->[[Documentation:Tutorial Section 2#Understanding POV-Ray's Coordinate System|Understanding POV-Ray's Coordinate System]]&quot;, you use
 
−
your right hand to determine the direction of rotations.</p>
 
−
<p>
 
−
In a two dimensional grid, x is always to the right and y is up. The two
 
−
versions of handedness arise from the question of whether z points into the
 
−
screen or out of it and which axis in your computer model relates to up in
 
−
the real world.</p>
 
−
<p>
 
−
Architectural CAD systems, like AutoCAD, tend to use the <em> God's
 
−
Eye</em> orientation that the z-axis is the elevation and is the model's
 
−
up direction. This approach makes sense if you are an architect looking at
 
−
a building blueprint on a computer screen. z means up, and it increases
 
−
towards you, with x and y still across and up the screen. This is the basic
 
−
right handed system.</p>
 
−
<p>
 
−
Stand alone rendering systems, like POV-Ray, tend to consider you as a
 
−
participant. You are looking at the screen as if you were a photographer
 
−
standing in the scene. The up direction in the model is now y, the same as up
 
−
in the real world and x is still to the right, so z must be depth, which
 
−
increases away from you into the screen. This is the basic left handed
 
−
system.</p>
 
−
 
−
 
−
I suggest editing the quite arbitrary handedness-"gymnastics" in this chapter (why should the thumb be Y, the index finger Z and the other fingers X?) to match those described in "Understanding POV-Ray's Coordinate System" (you don't have to be much of an acrobat either to exercise those).
 
−
 
−
I've added the text from that section. What changes did you have in mind? --[[User:Jholsenback|jholsenback]] 19:14, 21 June 2009 (UTC)
 
 
===Camera===
 
===Camera===
 
====Fisheye====
 
====Fisheye====
Line 77: Line 15:
 
</tr>
 
</tr>
 
</table>
 
</table>
−
 
+
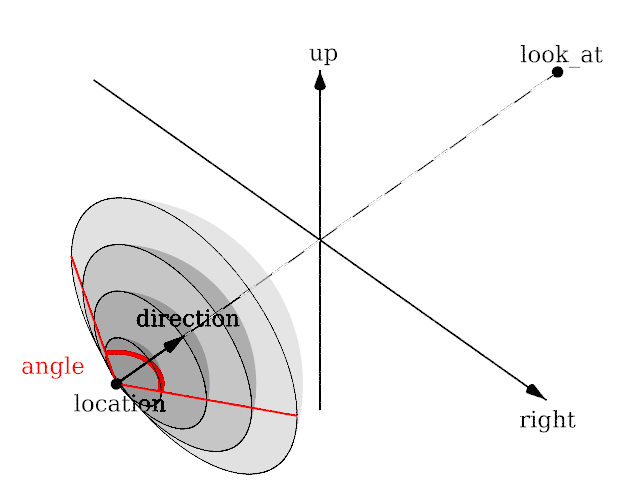
<p>Length of direction, up and right are irrelevant. Angle is the important setting and can go up to 360.</p>
−
Length of direction, up and right are irrelevant. Angle is the important setting and can go up to 360.
 
  
 
====omnimax====
 
====omnimax====
−
[[image:CameraViewOmnimax.png]]
+
<table class="centered" width="660px" cellpadding="0" cellspacing="10">
 +
<tr>
 +
<td>
 +
  [[Image:RefImgCameraViewOmnimax.png|center|640px<!--center--->]]
 +
</td>
 +
</tr>
 +
<tr>
 +
<td>
 +
  <p class="caption">The omnimax projection</p>
 +
</td>
 +
<td>
 +
</td>
 +
</tr>
 +
</table>
 +
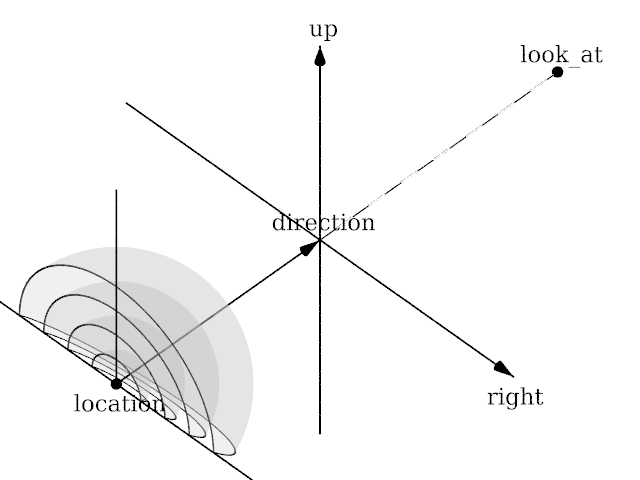
<p>Angle is irrelevant. The relative length of up and right are important.</p>
  
−
Angle is irrelevant. The relative length of up and right are important.
 
 
====orthographic====
 
====orthographic====
−
[[image:CameraViewOrthographic.png]]
+
<table class="centered" width="660px" cellpadding="0" cellspacing="10">
−
 
+
<tr>
−
Length of direction is irrelevant unless angle is used. Lengths of up and right define the dimensions of the view. Angle can be used (as long as less than 180) and will override the length of right and up (the aspect ratio between up and right will be kept nevertheless) with a scope of a perspective camera with the same direction and angle.
+
<td>
 +
  [[Image:RefImgCameraViewOrthographic.png|center|640px<!--center--->]]
 +
</td>
 +
</tr>
 +
<tr>
 +
<td>
 +
  <p class="caption">The orthographic projection</p>
 +
</td>
 +
<td>
 +
</td>
 +
</tr>
 +
</table>
 +
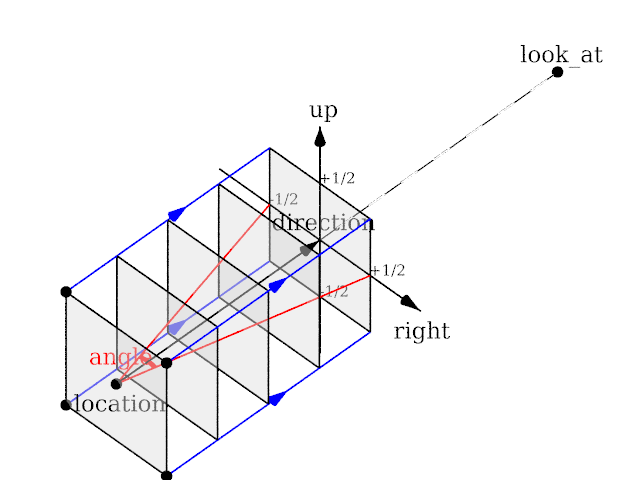
<p>Length of direction is irrelevant unless angle is used. Lengths of up and right define the dimensions of the view. Angle can be used (as long as less than 180) and will override the length of right and up (the aspect ratio between up and right will be kept nevertheless) with a scope of a perspective camera with the same direction and angle.</p>
 
====panoramic====
 
====panoramic====
−
[[image:CameraViewPanoramic.png]]
+
<table class="centered" width="660px" cellpadding="0" cellspacing="10">
−
 
+
<tr>
−
Angle is irrelevant. The relative length of direction, up and right are important as they defines the lengths of the 3 axis of the ellipsoid. With identical length and orthogonal vectors (both strongly recommended, unless used on purpose), it's identical to a spherical camera with angle 180,90.
+
<td>
 +
  [[Image:RefImgCameraViewPanoramic.png|center|640px<!--center--->]]
 +
</td>
 +
</tr>
 +
<tr>
 +
<td>
 +
  <p class="caption">The panoramic projection</p>
 +
</td>
 +
<td>
 +
</td>
 +
</tr>
 +
</table>
 +
<p>Angle is irrelevant. The relative length of direction, up and right are important as they defines the lengths of the 3 axis of the ellipsoid. With identical length and orthogonal vectors (both strongly recommended, unless used on purpose), it's identical to a spherical camera with angle 180,90.</p>
  
 
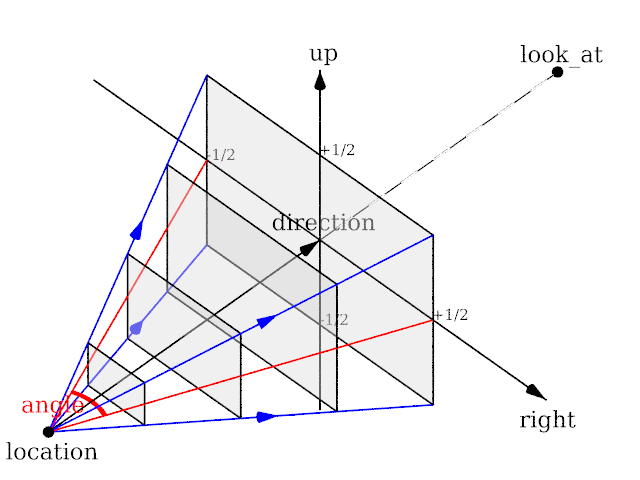
====perspective====
 
====perspective====
−
[[image:CameraViewPerspective.png]]
+
<table class="centered" width="660px" cellpadding="0" cellspacing="10">
 +
<tr>
 +
<td>
 +
  [[Image:RefImgCameraViewPerspective.png|center|640px<!--center--->]]
 +
</td>
 +
</tr>
 +
<tr>
 +
<td>
 +
  <p class="caption">The perspective projection</p>
 +
</td>
 +
<td>
 +
</td>
 +
</tr>
 +
</table>
 +
<p>Angle can be used as long as less than 180 and will recompute the length of right and up using direction, while keeping the aspect ratio between up and right. </p>
  
−
Angle can be used as long as less than 180 and will recompute the length of right and up using direction, while keeping the aspect ratio between up and right.
 
 
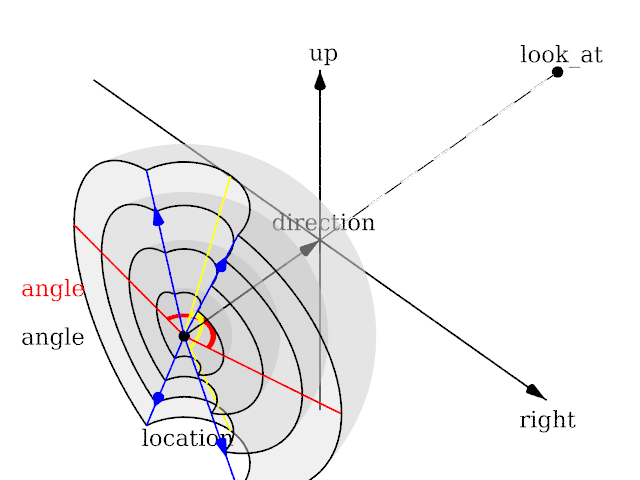
====spherical====
 
====spherical====
−
[[image:CameraViewSpherical.png]]
+
<table class="centered" width="660px" cellpadding="0" cellspacing="10">
−
 
+
<tr>
−
Lengths of direction, up and right vectors are irrelevant. Angle is the important setting, and it gets two values separated by a comma: the first is the horizontal angle, the second is the vertical angle. Both values can reach 360. If the second value is missing, it get half the value of the first.
+
<td>
 +
  [[Image:RefImgCameraViewSpherical.png|center|640px<!--center--->]]
 +
</td>
 +
</tr>
 +
<tr>
 +
<td>
 +
  <p class="caption">The spherical projection</p>
 +
</td>
 +
<td>
 +
</td>
 +
</tr>
 +
</table>
 +
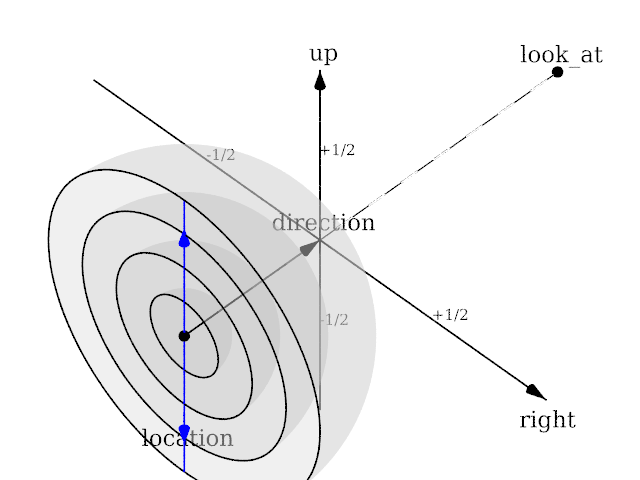
<p>Lengths of direction, up and right vectors are irrelevant. Angle is the important setting, and it gets two values separated by a comma: the first is the horizontal angle, the second is the vertical angle. Both values can reach 360. If the second value is missing, it get half the value of the first.</p>

Revision as of 02:11, 1 October 2011

Camera

Fisheye

RefImgCameraViewFisheye.png

The fisheye projection

Length of direction, up and right are irrelevant. Angle is the important setting and can go up to 360.

omnimax

RefImgCameraViewOmnimax.png

The omnimax projection

Angle is irrelevant. The relative length of up and right are important.

orthographic

RefImgCameraViewOrthographic.png

The orthographic projection

Length of direction is irrelevant unless angle is used. Lengths of up and right define the dimensions of the view. Angle can be used (as long as less than 180) and will override the length of right and up (the aspect ratio between up and right will be kept nevertheless) with a scope of a perspective camera with the same direction and angle.

panoramic

RefImgCameraViewPanoramic.png

The panoramic projection

Angle is irrelevant. The relative length of direction, up and right are important as they defines the lengths of the 3 axis of the ellipsoid. With identical length and orthogonal vectors (both strongly recommended, unless used on purpose), it's identical to a spherical camera with angle 180,90.

perspective

RefImgCameraViewPerspective.png

The perspective projection

Angle can be used as long as less than 180 and will recompute the length of right and up using direction, while keeping the aspect ratio between up and right.

spherical

RefImgCameraViewSpherical.png

The spherical projection

Lengths of direction, up and right vectors are irrelevant. Angle is the important setting, and it gets two values separated by a comma: the first is the horizontal angle, the second is the vertical angle. Both values can reach 360. If the second value is missing, it get half the value of the first.

Retrieved from "https://wiki.povray.org/content?title=Documentation_Talk:Reference_Section_3&oldid=4621"