Difference between revisions of "Reference:Torus"
Jholsenback (talk | contribs) m (1 revision: Initial Load (TF)) |
Jholsenback (talk | contribs) m (1 revision: Reference Migration Initial Load) |
(No difference)
| |
Revision as of 19:09, 15 March 2012
A torus is a 4th order quartic polynomial shape that looks
like a donut or inner tube. Because this shape is so useful and quartics are
difficult to define, POV-Ray lets you take a short-cut and define a torus
by:
TORUS:
torus {
Major, Minor
[TORUS_MODIFIER...]
}
TORUS_MODIFIER:
sturm | OBJECT_MODIFIER
Torus default values:
sturm : off
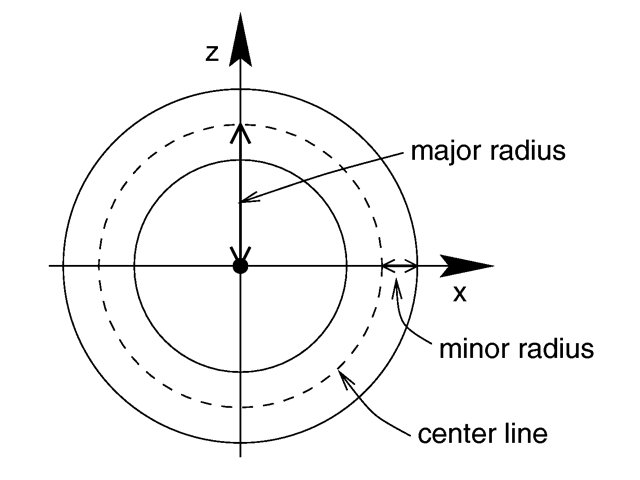
where Major is a float value giving the major radius
and Minor is a float specifying the minor radius. The
major radius extends from the center of the hole to the mid-line of the rim
while the minor radius is the radius of the cross-section of the rim. The
torus is centered at the origin and lies in the x-z-plane with the y-axis
sticking through the hole.
|
Major and minor radius of a torus. |
The torus is internally bounded by two cylinders and two rings forming a thick cylinder. With this bounding cylinder the performance of the torus intersection test is vastly increased. The test for a valid torus intersection, i.e. solving a 4th order polynomial, is only performed if the bounding cylinder is hit. Thus a lot of slow root solving calculations are avoided.
Calculations for all higher order polynomials must be very accurate. If the
torus renders improperly you may add the keyword sturm to use
POV-Ray's slower-yet-more-accurate Sturmian root solver.