Documentation:Tutorial Section 3.9
|
This document is protected, so submissions, corrections and discussions should be held on this documents talk page. |
SDL tutorial: A raytracer
The idea and the code
The idea is to raytrace a simple scene consisting of spheres and light sources into a 2-dimensional array containing color vectors which represents our "screen".
After this we just have to put those colors on the actual scene for POV-Ray to show them. This is made by creating a flat colored triangle mesh. The mesh is just flat like a plane with a color map on it. We could as well have written the result to a format like PPM and then read it and apply it as an image map to a plane, but this way we avoid a temporary file.
The following image is done with the raytracer SDL. It calculated the image at a resolution of 160x120 pixels and then raytraced an 512x384 image from it. This causes the image to be blurred and jagged (because it is practically "zoomed in" by a factor of 3.2). Calculating the image at 320x240 gives a much nicer result, but it is also much slower:
Note: there are no real spheres nor light sources here ("real" from the point of view of POV-Ray), just a flat colored triangle mesh (like a plane with a pigment on it) and a camera, nothing else.
Here is the source code of the raytracer; we will look it part by part through this tutorial.
#declare ImageWidth = 160;
#declare ImageHeight = 120;
#declare MaxRecLev = 5;
#declare AmbientLight = <.2,.2,.2>;
#declare BGColor = <0,0,0>;
// Sphere information.
// Values are:
// Center, <Radius, Reflection, 0>, Color, <phong_size, amount, 0>
#declare Coord = array[5][4]
{ {<-1.05,0,4>, <1,.5,0>, <1,.5,.25>, <40, .8, 0>}
{<1.05,0,4>, <1,.5,0>, <.5,1,.5>, <40, .8, 0>}
{<0,-3,5>, <2,.5,0>, <.25,.5,1>, <30, .4, 0>}
{<-1,2.3,9>, <2,.5,0>, <.5,.3,.1>, <30, .4, 0>}
{<1.3,2.6,9>, <1.8,.5,0>, <.1,.3,.5>, <30, .4, 0>}
}
// Light source directions and colors:
#declare LVect = array[3][2]
{ {<-1, 0, -.5>, <.8,.4,.1>}
{<1, 1, -.5>, <1,1,1>}
{<0,1,0>, <.1,.2,.5>}
}
//==================================================================
// Raytracing calculations:
//==================================================================
#declare MaxDist = 1e5;
#declare ObjAmnt = dimension_size(Coord, 1);
#declare LightAmnt = dimension_size(LVect, 1);
#declare Ind = 0;
#while(Ind < LightAmnt)
#declare LVect[Ind][0] = vnormalize(LVect[Ind][0]);
#declare Ind = Ind+1;
#end
#macro calcRaySphereIntersection(P, D, sphereInd)
#local V = P-Coord[sphereInd][0];
#local R = Coord[sphereInd][1].x;
#local DV = vdot(D, V);
#local D2 = vdot(D, D);
#local SQ = DV*DV-D2*(vdot(V, V)-R*R);
#if(SQ < 0) #local Result = -1;
#else
#local SQ = sqrt(SQ);
#local T1 = (-DV+SQ)/D2;
#local T2 = (-DV-SQ)/D2;
#local Result = (T1<T2 ? T1 : T2);
#end
Result
#end
#macro Trace(P, D, recLev)
#local minT = MaxDist;
#local closest = ObjAmnt;
// Find closest intersection:
#local Ind = 0;
#while(Ind < ObjAmnt)
#local T = calcRaySphereIntersection(P, D, Ind);
#if(T>0 & T<minT)
#local minT = T;
#local closest = Ind;
#end
#local Ind = Ind+1;
#end
// If not found, return background color:
#if(closest = ObjAmnt)
#local Pixel = BGColor;
#else
// Else calculate the color of the intersection point:
#local IP = P+minT*D;
#local R = Coord[closest][1].x;
#local Normal = (IP-Coord[closest][0])/R;
#local V = P-IP;
#local Refl = 2*Normal*(vdot(Normal, V)) - V;
// Lighting:
#local Pixel = AmbientLight;
#local Ind = 0;
#while(Ind < LightAmnt)
#local L = LVect[Ind][0];
// Shadowtest:
#local Shadowed = false;
#local Ind2 = 0;
#while(Ind2 < ObjAmnt)
#if(Ind2!=closest & calcRaySphereIntersection(IP,L,Ind2)>0)
#local Shadowed = true;
#local Ind2 = ObjAmnt;
#end
#local Ind2 = Ind2+1;
#end
#if(!Shadowed)
// Diffuse:
#local Factor = vdot(Normal, L);
#if(Factor > 0)
#local Pixel=Pixel+LVect[Ind][1]*Coord[closest][2]*Factor;
#end
// Specular:
#local Factor = vdot(vnormalize(Refl), L);
#if(Factor > 0)
#local Pixel =
Pixel +
LVect[Ind][1]*pow(Factor, Coord[closest][3].x)*
Coord[closest][3].y;
#end
#end
#local Ind = Ind+1;
#end
// Reflection:
#if(recLev < MaxRecLev & Coord[closest][1].y > 0)
#local Pixel =
Pixel + Trace(IP, Refl, recLev+1)*Coord[closest][1].y;
#end
#end
Pixel
#end
#debug "Rendering...\n\n"
#declare Image = array[ImageWidth][ImageHeight]
#declare IndY = 0;
#while(IndY < ImageHeight)
#declare CoordY = IndY/(ImageHeight-1)*2-1;
#declare IndX = 0;
#while(IndX < ImageWidth)
#declare CoordX =
(IndX/(ImageWidth-1)-.5)*2*ImageWidth/ImageHeight;
#declare Image[IndX][IndY] =
Trace(-z*3, <CoordX, CoordY, 3>, 1);
#declare IndX = IndX+1;
#end
#declare IndY = IndY+1;
#debug concat("\rDone ", str(100*IndY/ImageHeight, 0, 1),
"% (line ",str(IndY,0,0)," out of ",str(ImageHeight,0,0),")")
#end
#debug "\n"
//==================================================================
// Image creation (colored mesh):
//==================================================================
#default { finish { ambient 1 } }
#debug "Creating colored mesh to show image...\n"
mesh2
{ vertex_vectors
{ ImageWidth*ImageHeight*2,
#declare IndY = 0;
#while(IndY < ImageHeight)
#declare IndX = 0;
#while(IndX < ImageWidth)
<(IndX/(ImageWidth-1)-.5)*ImageWidth/ImageHeight*2,
IndY/(ImageHeight-1)*2-1, 0>,
<((IndX+.5)/(ImageWidth-1)-.5)*ImageWidth/ImageHeight*2,
(IndY+.5)/(ImageHeight-1)*2-1, 0>
#declare IndX = IndX+1;
#end
#declare IndY = IndY+1;
#end
}
texture_list
{ ImageWidth*ImageHeight*2,
#declare IndY = 0;
#while(IndY < ImageHeight)
#declare IndX = 0;
#while(IndX < ImageWidth)
texture { pigment { rgb Image[IndX][IndY] } }
#if(IndX < ImageWidth-1 & IndY < ImageHeight-1)
texture { pigment { rgb
(Image[IndX][IndY]+Image[IndX+1][IndY]+
Image[IndX][IndY+1]+Image[IndX+1][IndY+1])/4 } }
#else
texture { pigment { rgb 0 } }
#end
#declare IndX = IndX+1;
#end
#declare IndY = IndY+1;
#end
}
face_indices
{ (ImageWidth-1)*(ImageHeight-1)*4,
#declare IndY = 0;
#while(IndY < ImageHeight-1)
#declare IndX = 0;
#while(IndX < ImageWidth-1)
<IndX*2+ IndY *(ImageWidth*2),
IndX*2+2+IndY *(ImageWidth*2),
IndX*2+1+IndY *(ImageWidth*2)>,
IndX*2+ IndY *(ImageWidth*2),
IndX*2+2+IndY *(ImageWidth*2),
IndX*2+1+IndY *(ImageWidth*2),
<IndX*2+ IndY *(ImageWidth*2),
IndX*2+ (IndY+1)*(ImageWidth*2),
IndX*2+1+IndY *(ImageWidth*2)>,
IndX*2+ IndY *(ImageWidth*2),
IndX*2+ (IndY+1)*(ImageWidth*2),
IndX*2+1+IndY *(ImageWidth*2),
<IndX*2+ (IndY+1)*(ImageWidth*2),
IndX*2+2+(IndY+1)*(ImageWidth*2),
IndX*2+1+IndY *(ImageWidth*2)>,
IndX*2+ (IndY+1)*(ImageWidth*2),
IndX*2+2+(IndY+1)*(ImageWidth*2),
IndX*2+1+IndY *(ImageWidth*2),
<IndX*2+2+IndY *(ImageWidth*2),
IndX*2+2+(IndY+1)*(ImageWidth*2),
IndX*2+1+IndY *(ImageWidth*2)>,
IndX*2+2+IndY *(ImageWidth*2),
IndX*2+2+(IndY+1)*(ImageWidth*2),
IndX*2+1+IndY *(ImageWidth*2)
#declare IndX = IndX+1;
#end
#declare IndY = IndY+1;
#end
}
}
camera { orthographic location -z*2 look_at 0 }
Short introduction to raytracing
Before we start looking at the code, let's look briefly how raytracing works. This will help you understand what the script is doing.
The basic idea of raytracing is to "shoot" rays from the camera towards the scene and see what does the ray hit. If the ray hits the surface of an object then lighting calculations are performed in order to get the color of the surface at that place.
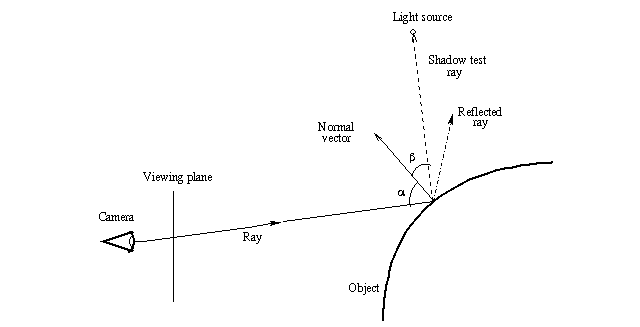
The following image shows this graphically:
First a ray is "shot" in a specified direction to see if there is something there. As this is solved mathematically, we need to know the mathematical representation of the ray and the objects in the scene so that we can calculate where does the ray intersect the objects. Once we get all the intersection points, we choose the closest one.
After this we have to calculate the lighting (ie. the illumination) of the object at the intersection point. In the most basic lighting model (as the one used in the script) there are three main things that affect the lighting of the surface:
- The shadow test ray, which determines whether a light source illuminates the intersection point or not.
- The normal vector, which is a vector perpendicular (ie. at 90 degrees) to the object surface at the intersection point. It determines the diffuse component of the lighting as well as the direction of the reflected ray (in conjunction with the incoming ray; that is, the angle alpha determines the direction of the reflected ray).
- The reflected ray, which determines the specular component of the lighting and of course the color of the reflection (if the object is reflective).
Do not worry if these things sound a bit confusing. Full details of all these things will be given through this tutorial, as we look what does the raytracing script do. The most important thing at this stage is to understand how the basic raytracing algorithm works at theoretical level (the image above should say most of it).
Let's just look at the raytracer source code line by line and look what does it do
Global settings
#declare ImageWidth = 160; #declare ImageHeight = 120; #declare MaxRecLev = 5; #declare AmbientLight = <.2,.2,.2>; #declare BGColor = <0,0,0>;
These lines just declare some identifiers defining some general values
which will be used later in the code. The keyword we use here is
#declare and it means that we are declaring a global identifier,
which will be seen in the whole code.
As you can see, we declare some identifiers to be of float type and others to be of vector type. The vector type identifiers are, in fact, used later for color definition (as their name implies).
The ImageWidth and ImageHeight define the
resolution of the image we are going to render.
Note: this only defines the resolution of the image we are going to render in our SDL (ie. into the array we will define later); it does not set the resolution of the image which POV-Ray will render.
The MaxRecLev limits the maximum number of recursive
reflections the code will calculate. It is equivalent to the
max_trace_level value in global_settings which
POV-Ray uses to raytrace.
The AmbientLight defines a color which is added to all
surfaces. This is used to "lighten up" shadowed parts so that they are not
completely dark. It is equivalent to the ambient_light value in
global_settings.
Finally, BGColor defines the color of the rays which do not
hit anything. It is equivalent to the background block of POV-Ray.
Scene definition
// Sphere information.
// Values are:
// Center, <Radius, Reflection, 0>, Color, <phong_size, amount, 0>
#declare Coord = array[5][4]
{ {<-1.05,0,4>, <1,.5,0>, <1,.5,.25>, <40, .8, 0>}
{<1.05,0,4>, <1,.5,0>, <.5,1,.5>, <40, .8, 0>}
{<0,-3,5>, <2,.5,0>, <.25,.5,1>, <30, .4, 0>}
{<-1,2.3,9>, <2,.5,0>, <.5,.3,.1>, <30, .4, 0>}
{<1.3,2.6,9>, <1.8,.5,0>, <.1,.3,.5>, <30, .4, 0>}
}
// Light source directions and colors:
#declare LVect = array[3][2]
{ {<-1, 0, -.5>, <.8,.4,.1>}
{<1, 1, -.5>, <1,1,1>}
{<0,1,0>, <.1,.2,.5>}
}
Here we use a bit more complex declarations: Array declarations.
In fact, they are even more complex than simple arrays, as we are declaring two-dimensional arrays.
A simple one-dimensional array can be declared like:
#declare MyArray = array[4] { 1, 2, 3, 4 }
and then values can be read from inside it with for example:
MyArray[2] (which will return 3 in this case as
the indexing starts from 0, ie. the index 0 gets the first value in the
array).
A two-dimensional array can be thought as an array containing arrays.
That is, if you say array[3][2], that means "an array which
has 3 elements; each one of those elements is an array with 2 elements".
When you want to read a value from it, for example MyArray[1][3],
you can think about it as "get the fourth value from the second array" (as
indexing starts from 0, then the index value 3 actually means "fourth value").
Note: although you can put almost anything inside an array (floats, vectors, objects and so on) you can only put one type of things inside an array. That is, you cannot mix float values and objects inside the same array. (One nice feature is that all POV-Ray objects are considered equivalent, which means that an object array can contain any objects inside it.)
What we are doing here is to define the information for our spheres and
light sources. The first array (called Coord) defines the
information for the spheres and the second (LVect) defines
the light sources.
For spheres we define their center as the first vector. The second
vector has both the radius of the sphere and its reflection amount
(which is equivalent to the reflection value in the
finish block of an object). This is a trick we use to
not to waste so much space, so we use two values of the same vector
for defining two different things.
The third vector defines the color of the sphere and the fourth the
specular component of the lighting (equivalent to phong_size
and phong values in the finish block of an
object).
The light source definition array contains direction vectors and colors. This means that the light sources are directional, that is, they just say which direction the light is coming from. It could have been equally easy to make point lights, though.
We will use the information inside these arrays later in order to raytrace the scene they define.
Initializing the raytracer
#declare MaxDist = 1e5; #declare ObjAmnt = dimension_size(Coord, 1); #declare LightAmnt = dimension_size(LVect, 1); #declare Ind = 0; #while(Ind < LightAmnt) #declare LVect[Ind][0] = vnormalize(LVect[Ind][0]); #declare Ind = Ind+1; #end
Before being able to start the raytracing, we have to intialize a couple of things.
The MaxDist defines the maximum distance a surface can
be from the starting point of a ray. This means that if a surface is farther
away from the starting point of the ray than this value, it will not be
seen. Strictly speaking this value is unnecessary and we can make the
raytracer so that there is no such a limitation, but we save one extra
step when we do it this way, and for scenes sized like ours it does not
really matter. (If you really, really want to get rid of the limitation,
I am sure you will figure out yourself how to do it after this tutorial.)
The ObjAmnt and LightAmnt identifiers are
declared just to make it easier for us to see how many objects and lights
are there (we need this info to loop through all the objects and lights).
Calling the dimension_size() function is a really nice way
of getting the number of items in an array.
All right, now we are getting to a bit more advanced stuff: What does the while-loop do there?
The #while-loop uses the Ind identifier as
an index value going from 0 to LightAmnt-1
(yes, -1; when Ind gets the value
LightAmnt the loop is ended right away). We also see that
we are indexing the LVect array; thus, it is clear we are
going through all the light sources (specifically through their direction
vectors, as we only use the [0] part) and we assign something
to them.
What we are doing is to assign a normalized version of each light source direction onto themselves, that is, just normalizing them.
Normalize is a synonym for "convert to unit vector", that is, convert to a vector with the same direction as the original but with length 1.
Why? We will later see that for illumination calculations we will be needing unit vectors. It is more efficient to convert the light source directions to unit vectors once at the beginning than every time for each pixel later.
Ray-sphere intersection
#macro calcRaySphereIntersection(P, D, sphereInd)
#local V = P-Coord[sphereInd][0];
#local R = Coord[sphereInd][1].x;
#local DV = vdot(D, V);
#local D2 = vdot(D, D);
#local SQ = DV*DV-D2*(vdot(V, V)-R*R);
#if(SQ < 0) #local Result = -1;
#else
#local SQ = sqrt(SQ);
#local T1 = (-DV+SQ)/D2;
#local T2 = (-DV-SQ)/D2;
#local Result = (T1<T2 ? T1 : T2);
#end
Result
#end
This is the core of the whole raytracing process.
First let's see how a macro works (if you know it, just skip the following section):
Inner workings of a #macro
A macro works like a substitution command (similar to the #define macros in the C programming language). The body of the macro is in practice inserted in the place where the macro is called. For example you can use a macro like this:
#macro UnitSphere()
sphere { 0,1 }
#end
object { UnitSphere() pigment { rgb 1 } }
The result of this code is, in effect, as if you had written:
object { sphere { 0,1 } pigment { rgb 1 } }
Of course there is no reason in making this, as you could have just #declared
the UnitSphere as a sphere of radius 1. However, the power of
macros kick in when you start using macro parameters. For example:
#macro Sphere(Radius)
sphere { 0, Radius }
#end
object { Sphere(3) pigment { rgb 1 } }
Now you can use the macro Sphere to create a sphere with
the specified radius. Of course this does not make much sense either, as
you could just write the sphere primitive directly because it is so short,
but this example is intentionally short to show how it works; the macros
become very handy when they create something much more complicated than
just a sphere.
There is one important difference between macros in POV-Ray and real
substitution macros: Any #local statement inside the macro
definition will be parsed at the visibility level of the macro only, that
is, it will have no effect on the environment where the macro was called
from. The following example shows what I am talking about:
#macro Sphere(Radius)
#local Color = <1,1,1>;
sphere { 0, Radius pigment { rgb Color } }
#end
#declare Color = <1,0,0>;
object { Sphere(3) }
// 'Color' is still <1,0,0> here,
// thus the following box will be red:
box { -1,1 pigment { rgb Color } }
In the example above, although the macro creates a local identifier
called Color and there is an identifier with the same name
at global level, the local definition does not affect the global one.
Also even if there was not any global definition of Color,
the one inside the macro is not seen outside it.
There is one important exception to this, and this is one of the most powerful features of macros (thanks to this they can be used as if they were functions): If an identifier (be it local or global) appears alone in the body of a macro (usually at the end), its value will be passed outside the macro (as if it was a return value). The following example shows how this works:
#macro Factorial(N)
#local Result = 1;
#local Ind = 2;
#while(Ind <= N)
#local Result = Result*Ind;
#local Ind = Ind+1;
#end
Result
#end
#declare Value = Factorial(5);
Although the identifier Result is local to the macro, its
value is passed as if it was a return value because of the last line of
the macro (where Result appears alone) and thus the identifier
Value will be set to the factorial of 5.
The ray-sphere intersection macro
Here is again the macro at the beginning of the page so that you do not have to scroll so much in order to see it:
#macro calcRaySphereIntersection(P, D, sphereInd)
#local V = P-Coord[sphereInd][0];
#local R = Coord[sphereInd][1].x;
#local DV = vdot(D, V);
#local D2 = vdot(D, D);
#local SQ = DV*DV-D2*(vdot(V, V)-R*R);
#if(SQ < 0) #local Result = -1;
#else
#local SQ = sqrt(SQ);
#local T1 = (-DV+SQ)/D2;
#local T2 = (-DV-SQ)/D2;
#local Result = (T1<T2 ? T1 : T2);
#end
Result
#end
The idea behind this macro is that it takes a starting point (ie. the starting point of the ray) a direction vector (the direction where the ray is shot) and an index to the sphere definition array defined previously. The macro returns a factor value; this value expresses how much we have to multiply the direction vector in order to hit the sphere.
This means that if the ray hits the specified sphere, the intersection
point will be located at:
StartingPoint + Result*Direction
The return value can be negative, which means that the intersection point was actually behind the starting point. A negative value will be just ignored, as if the ray did not hit anything. We can use this to make a little trick (which may seem obvious when said, but not so obvious when you have to figure it out for yourself): If the ray actually does not hit the sphere, we return just a negative value (does not really matter which).
And how does the macro do it? What is the theory behind those complicated-looking mathematical expressions?
I will use a syntax similar to POV-Ray syntax to express mathematical formulas here since that is probably the easiest way of doing it.
Let's use the following letters:
P = Starting point of the ray
D = Direction of the ray
C = Center of the sphere
R = Radius of the sphere
The theory behind the macro is that we have to see what is the value
T for which holds that:
vlength(P+T*D-C) = R
This means: The length of the vector between the center of the sphere
(C) and the intersection point (P+T*D) is equal
to the radius (R).
If we use an additional letter so that:
V = P-C
then the formula is reduced to:
vlength(T*D+V) = R
which makes our life easier. This formula can be opened as:
(T*Dx+Vx)2 +
(T*Dy+Vy)2 +
(T*Dz+Vz)2 - R2 = 0
Solving T from that is rather trivial math. We get a
2nd order polynomial which has two solutions (I will use the "·" symbol
to represent the dot-product of two vectors):
T = (-D·V ± sqrt((D·V)2 - D2(V2-R2))) / D2
Note: D2 means actually
D·D)
When the discriminant (ie. the expression inside the square root) is negative, the ray does not hit the sphere and thus we can return a negative value (the macro returns -1). We must check this in order to avoid the square root of a negative number error; as it has a very logical meaning in this case, the checking is natural.
If the value is positive, there are two solutions (or just one if the value is zero, but that does not really matter here), which corresponds to the two intersection points of the ray with the sphere.
As we get two values, we have to return the one which is smaller (the closest intersection). This is what this portion of the code does:
#local Result = (T1<T2 ? T1 : T2);
Note: this is an incomplete algorithm: If one value is negative and the other positive (this happens when the starting point is inside the sphere), we would have to return the positive one. The way it is now results in that we will not see the inner surface of the sphere if we put the camera inside one.
For our simple scene this is enough as we do not put our camera inside a sphere nor we have transparent spheres. We could add a check there which looks if one of the values is positive and the other negative and returns the positive one. However, this has an odd and very annoying result (you can try it if you want). This is most probably caused by the inaccuracy of floating point numbers and happens when calculating reflections (the starting point is exactly on the surface of the sphere). We could correct these problems by using epsilon values to get rid of accuracy problems, but in our simple scene this will not be necessary.
The Trace macro
#macro Trace(P, D, recLev)
If the ray-sphere intersection macro was the core of the raytracer, then the Trace-macro is practically everything else, the "body" of the raytracer.
The Trace-macro is a macro which takes the starting point of a ray, the direction of the ray and a recursion count (which should always be 1 when calling the macro from outside; 1 could be its default value if POV-Ray supported default values for macro parameters). It calculates and returns a color for that ray.
This is the macro we call for each pixel we want to calculate. That is, the starting point of the ray is our camera location and the direction is the direction of the ray starting from there and going through the "pixel" we are calculating. The macro returns the color of that pixel.
What the macro does is to see which sphere (if any) does the ray hit and then calculates the lighting for that intersection point (which includes calculating reflection), and returns the color.
The Trace-macro is recursive, meaning that it calls itself. More
specifically, it calls itself when it wants to calculate the ray reflected
from the surface of a sphere. The recLev value is used to stop
this recursion when the maximum recursion level is reached (ie. it calculates
the reflection only if recLev < MaxRecLev).
Let's examine this relatively long macro part by part:
Calculating the closest intersection
#local minT = MaxDist;
#local closest = ObjAmnt;
// Find closest intersection:
#local Ind = 0;
#while(Ind < ObjAmnt)
#local T = calcRaySphereIntersection(P, D, Ind);
#if(T>0 & T<minT)
#local minT = T;
#local closest = Ind;
#end
#local Ind = Ind+1;
#end
A ray can hit several spheres and we need the closest intersection point (and to know which sphere does it belong to). One could think that calculating the closest intersection is rather complicated, needing things like sorting all the intersection points and such. However, it is quite simple, as seen in the code above.
If we remember from the previous part, the ray-sphere intersection macro returns a factor value which tells us how much do we have to multiply the direction vector in order to get the intersection point. What we do is just to call the ray-sphere intersection macro for each sphere and take the smallest returned value (which is greater than zero).
First we initialize the minT identifier, which will hold
this smallest value to something big (this is where we need the
MaxDist value, although modifying this code to work around this
limitation is trivial and left to the user). Then we go through all the
spheres and call the ray-sphere intersection macro for each one. Then we
look if the returned value was greater than 0 and smaller than
minT, and if so, we assign the value to minT. When
the loop ends, we have the smallest intersection point in it.
Note: we also assign the index to the sphere which the closest
intersection belongs to in the closest identifier.
Here we use a small trick, and it is related to its initial value:
ObjAmnt. Why did we initialize it to that? The purpose of it
was to initialize it to some value which is not a legal index to a sphere
(ObjAmnt is not a legal index as the indices go from 0 to
ObjAmnt-1); a negative value would have worked as well, it
really does not matter. If the ray does not hit any sphere, then this identifier
is not changed and so we can see it afterwards.
If the ray doesn't hit anything
// If not found, return background color:
#if(closest = ObjAmnt)
#local Pixel = BGColor;
If the ray did not hit any sphere, what we do is just to return the
bacground color (defined by the BGColor identifier).
Initializing color calculations
Now comes one of the most interesting parts of the raytracing process: How do we calculate the color of the intersection point?
First we have to pre-calculate a couple of things:
#else
// Else calculate the color of the intersection point:
#local IP = P+minT*D;
#local R = Coord[closest][1].x;
#local Normal = (IP-Coord[closest][0])/R;
#local V = P-IP;
#local Refl = 2*Normal*(vdot(Normal, V)) - V;
Naturally we need the intersection point itself (needed to calculate the
normal vector and as the starting point of the reflected ray). This is
calculated into the IP identifier with the formula which I
have been repeating a few times during this tutorial.
Then we need the normal vector of the surface at the intersection point. A normal vector is a vector perpendicular (ie. at 90 degrees) to the surface. For a sphere this is very easy to calculate: It is just the vector from the center of the sphere to the intersection point.
Note: we normalize it (ie. convert it into a unit vector, ie. a vector of length 1) by dividing it by the radius of the sphere. The normal vector needs to be normalized for lighting calculation.
Now a tricky one: We need the direction of the reflected ray. This vector is of course needed to calculate the reflected ray, but it is also needed for specular lighting.
This is calculated into the Refl identifier in the code
above. What we do is to take the vector from the intersection point to
the starting point (P-IP) and "mirror" it with respect to
the normal vector. The formula for "mirroring" a vector V with
respect to a unit vector (let's call it Axis) is:
MirroredV = 2*Axis*(Axis·V) - V
(We could look at the theory behind this formula in more detail, but let's not go too deep into math in this tutorial, shall we?)
Going through the light sources
// Lighting:
#local Pixel = AmbientLight;
#local Ind = 0;
#while(Ind < LightAmnt)
#local L = LVect[Ind][0];
Now we can calculate the lighting of the intersection point. For this we need to go through all the light sources.
Note: L contains the direction vector which
points towards the light source, not its location.
We also initialize the color to be returned (Pixel) with
the ambient light value (given in the global settings part). The goal is to
add colors to this (the colors come from diffuse and specular lighting, and
reflection).
| Introduction | Shadow test |
|
This document is protected, so submissions, corrections and discussions should be held on this documents talk page. |