Documentation:Tutorial Section 2
|
This document is protected, so submissions, corrections and discussions should be held on this documents talk page. |
Getting Started
The beginning tutorial explains step by step how to use POV-Ray's scene description language to create your own scenes. The use of almost every feature of POV-Ray's language is explained in detail. We will learn basic things like placing cameras and light sources. We will also learn how to create a large variety of objects and how to assign different textures to them. The more sophisticated features like radiosity, interior, media and atmospheric effects will be explained in detail.
Our First Image
We will create the scene file for a simple picture. Since ray-tracers thrive on spheres, that is what we will render first.
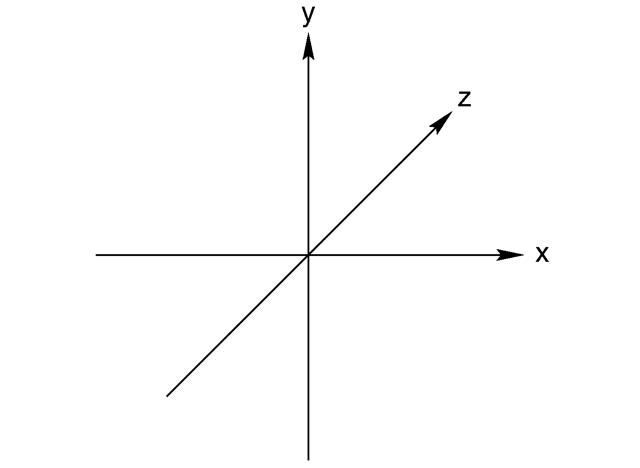
Understanding POV-Ray's Coordinate System
First, we have to tell POV-Ray where our camera is and where it is looking. To do this, we use 3D coordinates. The usual coordinate system for POV-Ray has the positive y-axis pointing up, the positive x-axis pointing to the right, and the positive z-axis pointing into the screen as follows:
This kind of coordinate system is called a left-handed coordinate system. If we use our left hand's fingers we can easily see why it is called left-handed. We just point our thumb in the direction of the positive x-axis (to the right), the index finger in the direction of the positive y-axis (straight up) and the middle finger in the positive z-axis direction (forward). We can only do this with our left hand. If we had used our right hand we would not have been able to point the middle finger in the correct direction.
The left hand can also be used to determine rotation directions. To do this we must perform the famous "Computer Graphics Aerobics" exercise. We hold up our left hand and point our thumb in the positive direction of the axis of rotation. Our fingers will curl in the positive direction of rotation. Similarly if we point our thumb in the negative direction of the axis our fingers will curl in the negative direction of rotation.
In the above illustration, the left hand is curling around the x-axis. The thumb points in the positive x direction and the fingers curl over in the positive rotation direction.
If we want to use a right-handed system, as some CAD systems and modelers
do, the right vector in the camera specification needs to be
changed. See the detailed description in "Handedness". In a
right-handed system we use our right hand for the "Aerobics".
There is some controversy over whether POV-Ray's method of doing a right-handed system is really proper. To avoid problems we stick with the left-handed system which is not in dispute.
Adding Standard Include Files
Using our personal favorite text editor, we create a file called demo.pov.
Some versions of POV-Ray come with their own built-in text editor which may be easier
to use. We then type in the following text. The input is case sensitive, so we have to be
sure to get capital and lowercase letters correct.
#include "colors.inc" // The include files contain #include "stones.inc" // pre-defined scene elements
The first include statement reads in definitions for various useful colors. The second include statement reads in a collection of stone textures. POV-Ray comes with many standard include files. Others of interest are:
#include "textures.inc" // pre-defined scene elements #include "shapes.inc" #include "glass.inc" #include "metals.inc" #include "woods.inc"
They read pre-defined textures, shapes, glass, metal, and wood textures. It is a good idea to have a look through them to see a few of the many possible shapes and textures available.
We should only include files we really need in our scene. Some of the
include files coming with POV-Ray are quite large and we should better save
the parsing time and memory if we do not need them. In the following
examples we will only use the colors.inc, and stones.inc
include files.
We may have as many include files as needed in a scene file. Include files may themselves contain include files, but we are limited to declaring includes nested only ten levels deep.
Filenames specified in the include statements will be searched for in the
current directory first. If it fails to find your .Inc files in the current
directory, POV-Ray searches any "library paths" that you have
specified. Library paths are options set by the +L command-line switch
or Library_Path option. See the chapter
"Setting POV-Ray Options"
for more information on library paths.
Because it is more useful to keep include files in a separate directory,
standard installations of POV-Ray place these files in the c:\povray3\include
directory (replace 'c:\povray3' with the actual directory that you installed
POV-Ray in). If you get an error message saying that POV-Ray cannot open
"colors.inc" or other include files, make sure that
you specify the library path properly.
Adding a Camera
The camera statement describes where and how the camera sees
the scene. It gives x-, y- and z-coordinates to indicate the position of the
camera and what part of the scene it is pointing at. We describe the
coordinates using a three-part vector. A vector is specified by
putting three numeric values between a pair of angle brackets and separating
the values with commas. We add the following camera statement to the
scene.
camera {
location <0, 2, -3>
look_at <0, 1, 2>
}
Briefly, location <0,2,-3> places the camera up two
units and back three units from the center of the ray-tracing universe which
is at <0,0,0>. By default +z is into the screen and -z is back out of
the screen.
Also look_at <0,1,2> rotates the camera to point at the
coordinates <0,1,2>. A point 1 unit up from the origin and 2 units away
from the origin. This makes it 5 units in front of and 1 unit lower than the
camera. The look_at point should be the center of attention of
our image.
Describing an Object
Now that the camera is set up to record the scene, let's place a yellow sphere into the scene. We add the following to our scene file:
sphere {
<0, 1, 2>, 2
texture {
pigment { color Yellow }
}
}
The first vector specifies the center of the sphere. In this example the x coordinate is zero so it is centered left and right. It is also at y=1 or one unit up from the origin. The z coordinate is 2 which is five units in front of the camera, which is at z=-3. After the center vector is a comma followed by the radius which in this case is two units. Since the radius is half the width of a sphere, the sphere is four units wide.
Adding Texture to an Object
After we have defined the location and size of the sphere, we need to
describe the appearance of the surface. The texture statement
specifies these parameters. Texture blocks describe the color, bumpiness and
finish properties of an object. In this example we will specify the color
only. This is the minimum we must do. All other texture options except color
will use default values.
The color we define is the way we want an object to look if fully
illuminated. If we were painting a picture of a sphere we would use dark
shades of a color to indicate the shadowed side and bright shades on the
illuminated side. However ray-tracing takes care of that for you. We only
need to pick the basic color inherent in the object and POV-Ray brightens or
darkens it depending on the lighting in the scene. Because we are defining
the basic color the object actually has rather than how it
looks the parameter is called pigment.
Many types of color patterns are available for use in a pigment statement.
The keyword color specifies that the whole object is to be one
solid color rather than some pattern of colors. We can use one of the color
identifiers previously defined in the standard include file
colors.inc.
If no standard color is available for our needs, we may define our own color
by using the color keyword followed by red, green,
and blue keywords specifying the amount of red, green and blue
to be mixed. For example a nice shade of pink can be specified by:
color red 1.0 green 0.8 blue 0.8
Note: the international - rather than American - form "colour" is also acceptable and may be used anywhere that "color" may be used.
The values after each keyword should be in the range from 0.0 to 1.0. Any of the three components not specified will default to 0. A shortcut notation may also be used. The following produces the same shade of pink:
color rgb <1.0, 0.8, 0.8>
In many cases the color keyword is superfluous, so the shortest way to
specify the pink color is:
rgb <1.0, 0.8, 0.8>
Colors are explained in more detail in section "Specifying Colors".
Defining a Light Source
One more detail is needed for our scene. We need a light source. Until we create one, there is no light in this virtual world. Thus we add the line
light_source { <2, 4, -3> color White}
to the scene file to get our first complete POV-Ray scene file as shown below.
#include "colors.inc"
background { color Cyan }
camera {
location <0, 2, -3>
look_at <0, 1, 2>
}
sphere {
<0, 1, 2>, 2
texture {
pigment { color Yellow }
}
}
light_source { <2, 4, -3> color White}
The vector in the light_source statement specifies the
location of the light as two units to our right, four units above the origin
and three units back from the origin. The light source is an invisible tiny
point that emits light. It has no physical shape, so no texture is
needed.
That's it! We close the file and render a small picture of it using whatever methods you used for your particular platform. If you specified a preview display it will appear on your screen. If you specified an output file (the default is file output on), then POV-Ray also created a file.
Note: if you do not have high color or true color display hardware then the preview image may look poor but the full detail is written to the image file regardless of the type of display.
The scene we just traced is not quite state of the art but we will have to start with the basics before we soon get to much more fascinating features and scenes.
Basic Shapes
So far we have just used the sphere shape. There are many other types of shapes that can be rendered by POV-Ray. The following sections will describe how to use some of the more simple objects as a replacement for the sphere used above.
Box Object
The box is one of the most common objects used. We try this
example in place of the sphere:
box {
<-1, 0, -1>, // Near lower left corner
< 1, 0.5, 3> // Far upper right corner
texture {
T_Stone25 // Pre-defined from stones.inc
scale 4 // Scale by the same amount in all
// directions
}
rotate y*20 // Equivalent to "rotate <0,20,0>"
}
In the example we can see that a box is defined by specifying the 3D coordinates of its opposite corners. The first vector is generally the minimum x-, y- and z-coordinates and the 2nd vector should be the maximum x-, y- and z-values however any two opposite corners may be used. Box objects can only be defined parallel to the axes of the world coordinate system. We can later rotate them to any angle.
Note: we can perform simple math on
values and vectors. In the rotate parameter we multiplied the vector
identifier y by 20. This is the same as <0,1,0>*20 or
<0,20,0>.
Cone Object
Here is another example showing how to use a cone:
cone {
<0, 1, 0>, 0.3 // Center and radius of one end
<1, 2, 3>, 1.0 // Center and radius of other end
texture { T_Stone25 scale 4 }
}
The cone shape is defined by the center and radius of each end. In this
example one end is at location <0,1,0> and has a radius of 0.3 while
the other end is centered at <1,2,3> with a radius of 1. If we want the
cone to come to a sharp point we must use radius=0. The solid end caps are
parallel to each other and perpendicular to the cone axis. If we want an open
cone with no end caps we have to add the keyword open after the
2nd radius like this:
cone {
<0, 1, 0>, 0.3 // Center and radius of one end
<1, 2, 3>, 1.0 // Center and radius of other end
open // Removes end caps
texture { T_Stone25 scale 4 }
}
Cylinder Object
We may also define a cylinder like this:
cylinder {
<0, 1, 0>, // Center of one end
<1, 2, 3>, // Center of other end
0.5 // Radius
open // Remove end caps
texture { T_Stone25 scale 4 }
}
Plane Object
Let's try out a computer graphics standard "The Checkered
Floor". We add the following object to the first version of the
demo.pov file, the one including the sphere.
plane { <0, 1, 0>, -1
pigment {
checker color Red, color Blue
}
}
The object defined here is an infinite plane. The vector <0,1,0> is the surface normal of the plane (i.e. if we were standing on the surface, the normal points straight up). The number afterward is the distance that the plane is displaced along the normal from the origin -- in this case, the floor is placed at y=-1 so that the sphere at y=1, radius=2, is resting on it.
Note: even though there is no texture statement there is
an implied texture here. We might find that continually typing statements
that are nested like texture {pigment} can get to be tiresome so
POV-Ray let's us leave out the texture statement under many
circumstances. In general we only need the texture block surrounding a
texture identifier (like the T_Stone25 example above), or when
creating layered textures (which are covered later).
This pigment uses the checker color pattern and specifies that the two colors red and blue should be used.
Because the vectors <1,0,0>, <0,1,0> and <0,0,1> are used
frequently, POV-Ray has three built-in vector identifiers x,
y and z respectively that can be used as a
shorthand. Thus the plane could be defined as:
plane { y, -1
pigment { ... }
}
Note: that we do not use angle brackets around vector identifiers.
Looking at the floor, we notice that the ball casts a shadow on the floor. Shadows are calculated very accurately by the ray-tracer, which creates precise, sharp shadows. In the real world, penumbral or "soft" shadows are often seen. Later we will learn how to use extended light sources to soften the shadows.
Torus Object
A torus can be thought of as a donut or an inner-tube. It is
a shape that is vastly useful in many kinds of CSG so POV-Ray has adopted
this 4th order quartic polynomial as a primitive shape. The syntax for a
torus is so simple that it makes it a very easy shape to work with once we
learn what the two float values mean. Instead of a lecture on the subject,
let's create one and do some experiments with it.
We create a file called tordemo.pov and edit it as follows:
#include "colors.inc"
camera {
location <0, .1, -25>
look_at 0
angle 30
}
background { color Gray50 } // to make the torus easy to see
light_source { <300, 300, -1000> White }
torus {
4, 1 // major and minor radius
rotate -90*x // so we can see it from the top
pigment { Green }
}
We trace the scene. Well, it is a donut alright. Let's try changing the major and minor radius values and see what happens. We change them as follows:
torus { 5, .25 // major and minor radius
That looks more like a hula-hoop! Let's try this:
torus { 3.5, 2.5 // major and minor radius
Whoa! A donut with a serious weight problem!
With such a simple syntax, there is not much else we can do to a torus besides change its texture... or is there? Let's see...
Tori are very useful objects in CSG. Let's try a little experiment. We make a difference of a torus and a box:
difference {
torus {
4, 1
rotate x*-90 // so we can see it from the top
}
box { <-5, -5, -1>, <5, 0, 1> }
pigment { Green }
}
Interesting... a half-torus. Now we add another one flipped the other way. Only, let's declare the original half-torus and the necessary transformations so we can use them again:
#declare Half_Torus = difference {
torus {
4, 1
rotate -90*x // so we can see it from the top
}
box { <-5, -5, -1>, <5, 0, 1> }
pigment { Green }
}
#declare Flip_It_Over = 180*x;
#declare Torus_Translate = 8; // twice the major radius
Now we create a union of two Half_Torus objects:
union {
object { Half_Torus }
object { Half_Torus
rotate Flip_It_Over
translate Torus_Translate*x
}
}
This makes an S-shaped object, but we cannot see the whole thing from our present camera. Let's add a few more links, three in each direction, move the object along the +z-direction and rotate it about the +y-axis so we can see more of it. We also notice that there appears to be a small gap where the half Tori meet. This is due to the fact that we are viewing this scene from directly on the x-z-plane. We will change the camera's y-coordinate from 0 to 0.1 to eliminate this.
union {
object { Half_Torus }
object { Half_Torus
rotate Flip_It_Over
translate x*Torus_Translate
}
object { Half_Torus
translate x*Torus_Translate*2
}
object { Half_Torus
rotate Flip_It_Over
translate x*Torus_Translate*3
}
object { Half_Torus
rotate Flip_It_Over
translate -x*Torus_Translate
}
object { Half_Torus
translate -x*Torus_Translate*2
}
object { Half_Torus
rotate Flip_It_Over
translate -x*Torus_Translate*3
}
object { Half_Torus
translate -x*Torus_Translate*4
}
rotate y*45
translate z*20
}
Rendering this we see a cool, undulating, snake-like something-or-other. Neato. But we want to model something useful, something that we might see in real life. How about a chain?
Thinking about it for a moment, we realize that a single link of a chain can
be easily modeled using two half tori and two cylinders. We create a new
file. We can use the same camera, background, light source and declared
objects and transformations as we used in tordemo.pov:
#include "colors.inc"
camera {
location <0, .1, -25>
look_at 0
angle 30
}
background { color Gray50 }
light_source{ <300, 300, -1000> White }
#declare Half_Torus = difference {
torus {
4,1
sturm
rotate x*-90 // so we can see it from the top
}
box { <-5, -5, -1>, <5, 0, 1> }
pigment { Green }
}
#declare Flip_It_Over = x*180;
#declare Torus_Translate = 8;
Now, we make a complete torus of two half tori:
union {
object { Half_Torus }
object { Half_Torus rotate Flip_It_Over }
}
This may seem like a wasteful way to make a complete torus, but we are really going to move each half apart to make room for the cylinders. First, we add the declared cylinder before the union:
#declare Chain_Segment = cylinder {
<0, 4, 0>, <0, -4, 0>, 1
pigment { Green }
}
We then add two Chain_Segments to the union and translate
them so that they line up with the minor radius of the torus on each
side:
union {
object { Half_Torus }
object { Half_Torus rotate Flip_It_Over }
object { Chain_Segment translate x*Torus_Translate/2 }
object { Chain_Segment translate -x*Torus_Translate/2 }
}
Now we translate the two half tori +y and -y so that the clipped ends meet
the ends of the cylinders. This distance is equal to half of the previously
declared Torus_Translate:
union {
object {
Half_Torus
translate y*Torus_Translate/2
}
object {
Half_Torus
rotate Flip_It_Over
translate -y*Torus_Translate/2
}
object {
Chain_Segment
translate x*Torus_Translate/2
}
object {
Chain_Segment
translate -x*Torus_Translate/2
}
}
We render this and voila! A single link of a chain. But we are not done yet! Whoever heard of a green chain? We would rather use a nice metallic color instead. First, we remove any pigment blocks in the declared tori and cylinders. Then we add a declaration for a golden texture just before the union that creates the link. Finally, we add the texture to the union and declare it as a single link:
#declare Half_Torus = difference {
torus {
4,1
sturm
rotate x*-90 // so we can see it from the top
}
box { <-5, -5, -1>, <5, 0, 1> }
}
#declare Chain_Segment = cylinder {
<0, 4, 0>, <0, -4, 0>, 1
}
#declare Chain_Gold = texture {
pigment { BrightGold }
finish {
ambient .1
diffuse .4
reflection .25
specular 1
metallic
}
}
#declare Link = union {
object {
Half_Torus
translate y*Torus_Translate/2
}
object {
Half_Torus
rotate Flip_It_Over
translate -y*Torus_Translate/2
}
object {
Chain_Segment
translate x*Torus_Translate/2
}
object {
Chain_Segment
translate -x*Torus_Translate/2
} texture { Chain_Gold }
}
Now we make a union of two links. The second one will have to be
translated +y so that its inner wall just meets the inner wall of the other
link, just like the links of a chain. This distance turns out to be double
the previously declared Torus_Translate minus 2 (twice the minor
radius). This can be described by the expression:
Torus_Translate*2-2*y
We declare this expression as follows:
#declare Link_Translate = Torus_Translate*2-2*y;
In the object block, we will use this declared value so that we can
multiply it to create other links. Now, we rotate the second link
90*y so that it is perpendicular to the first, just like links of a
chain. Finally, we scale the union by 1/4 so that we can see the whole
thing:
union {
object { Link }
object { Link translate y*Link_Translate rotate y*90 }
scale .25
}
We render this and we will see a very realistic pair of links. If we want to make an entire chain, we must declare the above union and then create another union of this declared object. We must be sure to remove the scaling from the declared object:
#declare Link_Pair =
union {
object { Link }
object { Link translate y*Link_Translate rotate y*90 }
}
Now we declare our chain:
#declare Chain = union {
object { Link_Pair}
object { Link_Pair translate y*Link_Translate*2 }
object { Link_Pair translate y*Link_Translate*4 }
object { Link_Pair translate y*Link_Translate*6 }
object { Link_Pair translate -y*Link_Translate*2 }
object { Link_Pair translate -y*Link_Translate*4 }
object { Link_Pair translate -y*Link_Translate*6 }
}
And finally we create our chain with a couple of transformations to make it easier to see. These include scaling it down by a factor of 1/10, and rotating it so that we can clearly see each link:
object { Chain scale .1 rotate <0, 45, -45> }
We render this and we should see a very realistic gold chain stretched diagonally across the screen.
CSG Objects
Constructive Solid Geometry, or CSG, is a powerful tool to combine primitive objects to create more complex objects as shown in the following sections.
What is CSG?
CSG stands for Constructive Solid Geometry. POV-Ray
allows us to construct complex solids by combining primitive shapes in four
different ways. In the union statement, two or more shapes are
added together. With the intersection statement, two or more
shapes are combined to make a new shape that consists of the area common to
both shapes. The difference statement, an initial shape has all
subsequent shapes subtracted from it.
And last but not least merge, which is like a union where the
surfaces inside the union are removed (useful in transparent CSG objects). We
will deal with each of these in detail in the next few sections.
CSG objects can be extremely complex. They can be deeply nested. In other words there can be unions of differences or intersections of merges or differences of intersections or even unions of intersections of differences of merges... ad infinitum. CSG objects are (almost always) finite objects and thus respond to auto-bounding and can be transformed like any other POV primitive shape.
CSG Union
Let's try making a simple union. Create a file called
csgdemo.pov and edit it as follows:
#include "colors.inc"
camera {
location <0, 1, -10>
look_at 0
angle 36
}
light_source { <500, 500, -1000> White }
plane { y, -1.5
pigment { checker Green White }
}
Let's add two spheres each translated 0.5 units along the x-axis in each direction. We color one blue and the other red.
sphere { <0, 0, 0>, 1
pigment { Blue }
translate -0.5*x
}
sphere { <0, 0, 0>, 1
pigment { Red }
translate 0.5*x
}
We trace this file and note the results. Now we place a union block around the two spheres. This will create a single CSG union out of the two objects.
union{
sphere { <0, 0, 0>, 1
pigment { Blue }
translate -0.5*x
}
sphere { <0, 0, 0>, 1
pigment { Red }
translate 0.5*x
}
}
We trace the file again. The union will appear no different from what each sphere looked like on its own, but now we can give the entire union a single texture and transform it as a whole. Let's do that now.
union{
sphere { <0, 0, 0>, 1
translate -0.5*x
}
sphere { <0, 0, 0>, 1
translate 0.5*x
}
pigment { Red }
scale <1, .25, 1>
rotate <30, 0, 45>
}
We trace the file again. As we can see, the object has changed dramatically. We experiment with different values of scale and rotate and try some different textures.
There are many advantages of assigning only one texture to a CSG object instead of assigning the texture to each individual component. First, it is much easier to use one texture if our CSG object has a lot of components because changing the objects appearance involves changing only one single texture. Second, the file parses faster because the texture has to be parsed only once. This may be a great factor when doing large scenes or animations. Third, using only one texture saves memory because the texture is only stored once and referenced by all components of the CSG object. Assigning the texture to all n components means that it is stored n times.
| Notation and Basic Assumptions | CSG Intersection |
|
This document is protected, so submissions, corrections and discussions should be held on this documents talk page. |