Reference:Warp
The warp statement is a pattern modifier that is similar to
turbulence. Turbulence works by taking the pattern evaluation point and
pushing it about in a series of random steps. However warps push the point in
very well-defined, non-random, geometric ways. The warp
statement also overcomes some limitations of traditional turbulence and
transformations by giving the user more control over the order in which
turbulence, transformation and warp modifiers are applied to the pattern.
The turbulence warp provides an alternative way to specify turbulence. The others modify the pattern in geometric ways.
The syntax for using a warp statement is:
WARP:
warp { WARP_ITEM }
WARP_ITEM:
repeat <Direction> [REPEAT_ITEMS...] |
black_hole <Location>, Radius [BLACK_HOLE_ITEMS...] |
turbulence <Amount> [TURB_ITEMS...]
cylindrical [ orientation VECTOR | dist_exp FLOAT ]
spherical [ orientation VECTOR | dist_exp FLOAT ]
toroidal [ orientation VECTOR | dist_exp FLOAT | major_radius FLOAT ]
planar [ VECTOR , FLOAT ]
REPEAT_ITEMS:
offset <Amount> |
flip <Axis>
BLACK_HOLE_ITEMS:
strength Strength | falloff Amount | inverse |
repeat <Repeat> | turbulence <Amount>
TURB_ITEMS:
octaves Count | omega Amount | lambda Amount
You may have as many separate warp statements as you like in each pattern.
The placement of warp statements relative to other modifiers such as
color_map or turbulence is not important. However
placement of warp statements relative to each other and to transformations is
significant. Multiple warps and transformations are evaluated in the order in
which you specify them. For example if you translate, then warp or warp, then
translate, the results can be different.
Black Hole Warp
A black_hole warp is so named because of its similarity to
real black holes. Just like the real thing, you cannot actually see a black
hole. The only way to detect its presence is by the effect it has on things
that surround it.
Take, for example, a wood grain. Using POV-Ray's normal turbulence and other texture modifier functions, you can get a nice, random appearance to the grain. But in its randomness it is regular - it is regularly random! Adding a black hole allows you to create a localized disturbance in a wood grain in either one or multiple locations. The black hole can have the effect of either sucking the surrounding texture into itself (like the real thing) or pushing it away. In the latter case, applied to a wood grain, it would look to the viewer as if there were a knothole in the wood. In this text we use a wood grain regularly as an example, because it is ideally suitable to explaining black holes. However, black holes may in fact be used with any texture or pattern. The effect that the black hole has on the texture can be specified. By default, it sucks with the strength calculated exponentially (inverse-square). You can change this if you like.
Black holes may be used anywhere a warp is permitted. The syntax is:
BLACK_HOLE_WARP:
warp {
black_hole <Location>, Radius
[BLACK_HOLE_ITEMS...]
}
BLACK_HOLE_ITEMS:
strength Strength | falloff Amount | inverse | type Type |
repeat <Repeat> | turbulence <Amount>
The minimal requirement is the black_hole keyword followed by
a vector <Location> followed by a comma and a
float Radius. Black holes effect all points within the
spherical region around the location and within the radius. This is
optionally followed by any number of other keywords which control how the
texture is warped.
The falloff keyword may be used with a float value to specify
the power by which the effect of the black hole falls off. The default is
two. The force of the black hole at any given point, before applying the
strength modifier, is as follows.
First, convert the distance from the point to the center to a proportion (0 to 1) that the point is from the edge of the black hole. A point on the perimeter of the black hole will be 0.0; a point at the center will be 1.0; a point exactly halfway will be 0.5, and so forth. Mentally you can consider this to be a closeness factor. A closeness of 1.0 is as close as you can get to the center (i.e. at the center), a closeness of 0.0 is as far away as you can get from the center and still be inside the black hole and a closeness of 0.5 means the point is exactly halfway between the two.
Call this value c. Raise c to the power specified in falloff.
By default Falloff is 2, so this is c^2 or c squared. The resulting value is
the force of the black hole at that exact location and is used, after
applying the strength scaling factor as described below, to
determine how much the point is perturbed in space. For example, if c is 0.5
the force is 0.5^2 or 0.25. If c is 0.25 the force is 0.125. But if c is
exactly 1.0 the force is 1.0. Recall that as c gets smaller the point is
farther from the center of the black hole. Using the default power of 2, you
can see that as c reduces, the force reduces exponentially in an
inverse-square relationship. Put in plain English, it means that the force is
much stronger (by a power of two) towards the center than it is at the
outside.
By increasing falloff, you can increase the magnitude of the
falloff. A large value will mean points towards the perimeter will hardly be
affected at all and points towards the center will be affected strongly. A
value of 1.0 for falloff will mean that the effect is linear. A
point that is exactly halfway to the center of the black hole will be
affected by a force of exactly 0.5. A value of falloff of less
than one but greater than zero means that as you get closer to the outside,
the force increases rather than decreases. This can have some uses but there
is a side effect. Recall that the effect of a black hole ceases outside its
perimeter. This means that points just within the perimeter will be affected
strongly and those just outside not at all. This would lead to a visible
border, shaped as a sphere. A value for falloff of 0 would mean
that the force would be 1.0 for all points within the black hole, since any
number larger 0 raised to the power of 0 is 1.0.
The strength keyword may be specified with a float value to
give you a bit more control over how much a point is perturbed by the black
hole. Basically, the force of the black hole (as determined above) is
multiplied by the value of strength, which defaults to 1.0. If
you set strength to 0.5, for example, all points within the black hole will
be moved by only half as much as they would have been. If you set it to 2.0
they will be moved twice as much.
There is a rider to the latter example, though - the movement is clipped to
a maximum of the original distance from the center. That is to say, a point
that is 0.75 units from the center may only be moved by a maximum of 0.75
units either towards the center or away from it, regardless of the value of
strength. The result of this clipping is that you will have an
exclusion area near the center of the black hole where all points whose final
force value exceeded or equaled 1.0 were moved by a fixed amount.
If the inverse keyword is specified then the points
pushed away from the center instead of being pulled in.
The repeat keyword followed by a vector, allows you to simulate
the effect of many black holes without having to explicitly declare them.
Repeat is a vector that tells POV-Ray to use this black hole at multiple
locations. Using repeat logically divides your scene up into
cubes, the first being located at <0,0,0> and going to
<Repeat>. Suppose your repeat vector was <1,5,2>. The
first cube would be from <0,0,0> to < 1,5,2>. This cube repeats,
so there would be one at < -1,-5,-2>, <1,5,2>, <2,10,4> and
so forth in all directions, ad infinitum.
When you use repeat, the center of the black hole does not
specify an absolute location in your scene but an offset into each block. It
is only possible to use positive offsets. Negative values will produce
undefined results.
Suppose your center was <0.5,1,0.25> and the repeat vector is <2,2,2>. This gives us a block at < 0,0,0> and <2,2,2>, etc. The centers of the black hole's for these blocks would be <0,0,0> + < 0.5,1.0,0.25>, i. e. <0.5,1.0,0.25>, and < 2,2,2> + <0.5,1.0,0.25>, i. e. < 2,5,3.0,2.25>.
Due to the way repeats are calculated internally, there is a restriction on the values you specify for the repeat vector. Basically, each black hole must be totally enclosed within each block (or cube), with no part crossing into a neighboring one. This means that, for each of the x, y and z dimensions, the offset of the center may not be less than the radius, and the repeat value for that dimension must be >=the center plus the radius since any other values would allow the black hole to cross a boundary. Put another way, for each of x, y and z
Radius <= Offset or Center <= Repeat - Radius.
If the repeat vector in any dimension is too small to fit this criteria, it will be increased and a warning message issued. If the center is less than the radius it will also be moved but no message will be issued.
Note that none of the above should be read to mean that you cannot
overlap black holes. You most certainly can and in fact this can produce some
most useful effects. The restriction only applies to elements of the
same black hole which is repeating. You can declare a second black
hole that also repeats and its elements can quite happily overlap the first
and causing the appropriate interactions. It is legal for the repeat value
for any dimension to be 0, meaning that POV-Ray will not repeat the black
hole in that direction.
The turbulence can only be used in a black hole with
repeat. It allows an element of randomness to be inserted into the way
the black holes repeat, to cause a more natural look. A good example would be
an array of knotholes in wood - it would look rather artificial if each
knothole were an exact distance from the previous.
The turbulence vector is a measurement that is added to each
individual black hole in an array, after each axis of the vector is multiplied
by a different random amount ranging from 0 to 1. The resulting actual
position of the black hole's center for that particular repeat element is
random (but consistent, so renders will be repeatable) and somewhere within
the above coordinates. There is a rider on the use of turbulence, which
basically is the same as that of the repeat vector. You cannot specify a
value which would cause a black hole to potentially cross outside of its
particular block.
In summary: For each of x, y and z the offset of the center must be >=radius and the value of the repeat must be >= center + radius + turbulence. The exception being that repeat may be 0 for any dimension, which means do not repeat in that direction.
Some examples are given by
warp {
black_hole <0, 0, 0>, 0.5
}
warp {
black_hole <0.15, 0.125, 0>, 0.5
falloff 7
strength 1.0
repeat <1.25, 1.25, 0>
turbulence <0.25, 0.25, 0>
inverse
}
warp {
black_hole <0, 0, 0>, 1.0
falloff 2
strength 2
inverse
}
Repeat Warp
The repeat warp causes a section of the pattern to be
repeated over and over. It takes a slice out of the pattern and makes
multiple copies of it side-by-side. The warp has many uses but was originally
designed to make it easy to model wood veneer textures. Veneer is made by
taking very thin slices from a log and placing them side-by-side on some
other backing material. You see side-by-side nearly identical ring patterns
but each will be a slice perhaps 1/32th of an inch deeper.
The syntax for a repeat warp is
REPEAT_WARP:
warp { repeat <Direction> [REPEAT_ITEMS...] }
REPEAT_ITEMS:
offset <Amount> | flip <Axis>
The repeat vector specifies the direction in which the
pattern repeats and the width of the repeated area. This vector must lie
entirely along an axis. In other words, two of its three components must be
0. For example
pigment {
wood
warp { repeat 2*x }
}
which means that from x=0 to x=2 you get whatever the pattern usually is.
But from x=2 to x=4 you get the same thing exactly shifted two units over in
the x-direction. To evaluate it you simply take the x-coordinate modulo 2.
Unfortunately you get exact duplicates which is not very realistic. The
optional offset vector tells how much to translate the pattern
each time it repeats. For example
pigment {
wood
warp {repeat x*2 offset z*0.05}
}
means that we slice the first copy from x=0 to x=2 at z=0 but at x=2 to x=4 we offset to z=0.05. In the 4 to 6 interval we slice at z=0.10. At the n-th copy we slice at 0.05 n z. Thus each copy is slightly different. There are no restrictions on the offset vector.
Finally the flip vector causes the pattern to be flipped or
mirrored every other copy of the pattern. The first copy of the pattern in
the positive direction from the axis is not flipped. The next farther is, the
next is not, etc. The flip vector is a three component x, y, z vector but
each component is treated as a boolean value that tells if you should or
should not flip along a given axis. For example
pigment {
wood
warp {repeat 2*x flip <1,1,0>}
}
means that every other copy of the pattern will be mirrored about the x- and y- axis but not the z-axis. A non-zero value means flip and zero means do not flip about that axis. The magnitude of the values in the flip vector does not matter.
Turbulence Warp
Inside the warp statement, the keyword turbulence followed by a float or vector may be
used to stir up any pigment, normal or density. A number of
optional parameters may be used with turbulence to control how it is
computed. The syntax is:
TURBULENCE_ITEM: turbulence <Amount> | octaves Count | omega Amount | lambda Amount
Typical turbulence values range from the default 0.0, which is no turbulence, to 1.0 or more, which is very turbulent. If a vector is specified different amounts of turbulence are applied in the x-, y- and z-direction. For example
turbulence <1.0, 0.6, 0.1>
has much turbulence in the x-direction, a moderate amount in the y-direction and a small amount in the z-direction.
Turbulence uses a random noise function called DNoise. This is
similar to the noise used in the bozo pattern except that
instead of giving a single value it gives a direction. You can think of it as
the direction that the wind is blowing at that spot. Points close together
generate almost the same value but points far apart are randomly
different.
Turbulence uses DNoise to push a point around in several steps
called octaves. We locate the point we want to evaluate, then
push it around a bit using turbulence to get to a different point then look
up the color or pattern of the new point.
It says in effect Do not give me the color at this spot... take a few random steps in different directions and give me that color. Each step is typically half as long as the one before. For example:
|
The magnitude of these steps is controlled by the turbulence value. There are three additional parameters which control how turbulence is computed. They are |
|
|
Turbulence random walk. |
Octaves
The octaves keyword may be followed by an integer value to
control the number of steps of turbulence that are computed. Legal values
range from 1 to <10. The default value of 6 is a fairly high value; you
will not see much change by setting it to a higher value because the extra
steps are too small. Float values are truncated to integer. Smaller numbers
of octaves give a gentler, wavy turbulence and computes faster. Higher
octaves create more jagged or fuzzy turbulence and takes longer to
compute.
Lambda
The lambda parameter controls how statistically different the
random move of an octave is compared to its previous octave. The default
value is 2.0 which is quite random. Values close to lambda 1.0 will
straighten out the randomness of the path in the diagram above. The zig-zag
steps in the calculation are in nearly the same direction. Higher values can
look more swirly under some circumstances.
Omega
The omega value controls how large each successive octave
step is compared to the previous value. Each successive octave of turbulence
is multiplied by the omega value. The default omega 0.5 means
that each octave is 1/2 the size of the previous one. Higher omega values
mean that 2nd, 3rd, 4th and up octaves contribute more turbulence giving a
sharper, crinkly look while smaller omegas give a fuzzy kind of
turbulence that gets blurry in places.
Mapping using warps
With the cylindrical, spherical and toroidal warps you can wrap checkers,
bricks and other patterns around cylinders, spheres, tori and other objects. In essence, these
warps use the same mapping as the image maps use.
The syntax is as follows:
CYLINDRICAL_WARP:
warp { cylindrical [CYLINDRICAL_ITEMS...]}
CYLINDRICAL_ITEMS:
orientation VECTOR | dist_exp FLOAT
SPHERICAL_WARP:
warp { spherical [SPHERICAL_ITEMS...]}
SPHERICAL_ITEMS:
orientation VECTOR | dist_exp FLOAT
TOROIDAL_WARP:
warp { toroidal [TOROIDAL_ITEMS...]}
TOROIDAL_ITEMS:
orientation VECTOR | dist_exp FLOAT | major_radius FLOAT
PLANAR_WARP:
warp { planar [ VECTOR , FLOAT ]}
CUBIC_WARP:
warp { cubic }
These defaults are in affect:
orientation <0,0,1> dist_exp 0 major_radius 1
Although these warps do 3D mapping, some concession had to be made on depth.
The distance exponent is controlled by using the dist_exp keyword. When using the default value of 0, imagine a box from <0,0> to <1,1> stretching to infinity along the orientation vector.
The distance keyword is evaluated as follows:
sphere: distance from origincylinder: distance from y-axistorus: distance from major radius
The planar warp was made to make a pattern act like an image_map, of infinite size and can be useful in combination with other mapping-warps. By default the pigment in the XY-plane is extruded along
the Z-axis. The pigment can be taken from an other plane, by specifying the optional vector (normal of the plane) and float (distance along the normal). The result, again, is extruded along the Z-axis.
The cubic warp requires no parameters, and maps an area in the x-y plane between <0,0> and <1,1> around the origin in the same way as uv-mapping an origin-centered cube-shaped box would. The cubic warp works with any object whereas the uv-mapping only works for the box object. See the section on box uv-mapping for details.
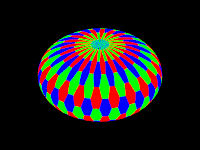
The following code examples produced the images below:
torus {
1, 0.5
pigment {
hexagon
scale 0.1
warp {
toroidal
orientation y
dist_exp 1
major_radius 1
}
}
}
sphere {
0,1
pigment {
hexagon
scale <0.5/pi, 1, 1/pi>*0.1
warp {
spherical
orientation y
dist_exp 1
}
}
}
cylinder {
-y, y, 1
pigment {
hexagon
scale <0.5/pi, 1, 1>*0.1
warp {
cylindrical
orientation y
dist_exp 1
}
}
}
|
cylindrical warp |
spherical warp |
toroidal warp |
Turbulence versus Turbulence Warp
The POV-Ray language contains an ambiguity and limitation on the way you
specify turbulence and transformations such as
translate, rotate, scale,
matrix, and transform transforms. Usually the turbulence
is done first. Then all translate, rotate, scale, matrix, and transform
operations are always done after turbulence regardless of the order in which
you specify them. For example this
pigment {
wood
scale .5
turbulence .2
}
works exactly the same as
pigment {
wood
turbulence .2
scale .5
}
The turbulence is always first. A better example of this limitation is with uneven turbulence and rotations.
pigment {
wood
turbulence 0.5*y
rotate z*60
}
// as compared to
pigment {
wood
rotate z*60
turbulence 0.5*y
}
The results will be the same either way even though you would think it should look different.
We cannot change this basic behavior in POV-Ray now because lots of scenes would potentially render differently if suddenly the order transformation vs. turbulence mattered when in the past, it did not.
However, by specifying our turbulence inside warp statement you tell POV-Ray that the order in which turbulence, transformations and other warps are applied is significant. Here is an example of a turbulence warp.
warp { turbulence <0,1,1> octaves 3 lambda 1.5 omega 0.3 }
The significance is that this
pigment {
wood
translate <1,2,3> rotate x*45 scale 2
warp { turbulence <0,1,1> octaves 3 lambda 1.5 omega 0.3 }
}
produces different results than this...
pigment {
wood
warp { turbulence <0,1,1> octaves 3 lambda 1.5 omega 0.3 }
translate <1,2,3> rotate x*45 scale 2
}
You may specify turbulence without using a warp statement. However you cannot control the order in which they are evaluated unless you put them in a warp.
The evaluation rules are as follows:
- First any turbulence not inside a warp statement is applied regardless of the order in which it appears relative to warps or transformations.
- Next each warp statement, translate, rotate, scale or matrix one-by-one, is applied in the order the user specifies. If you want turbulence done in a specific order, you simply specify it inside a warp in the proper place.
Turbulence
The turbulence pattern modifier is still supported for compatibility
issues, but it is better nowadays to use the warp turbulence feature,
which does not have turbulence's limitation in transformation order
(turbulence is always applied first, before any scale, translate or
rotate, whatever the order you specify). For a detailed discussion see
Turbulence versus Turbulence Warp
The old-style turbulence is handled slightly differently when used with the agate, marble, spiral1, spiral2, and wood textures.