Difference between revisions of "Reference Talk:Tiling Pattern"
(Adding table of tiling to unit square scaling vectors.) |
m (Table border to 5px) |
||
| Line 29: | Line 29: | ||
<p>The scale required to fit the core repeated tile into a unit square size for each tiling pattern is given in the table below.</p> | <p>The scale required to fit the core repeated tile into a unit square size for each tiling pattern is given in the table below.</p> | ||
| − | <table class="centered" cellpadding="5" cellspacing="0" border=" | + | <table class="centered" cellpadding="5" cellspacing="0" border="5" border-collapse="collapse"> |
<tr> | <tr> | ||
<th>Tiling Number</th> | <th>Tiling Number</th> | ||
Revision as of 14:47, 25 September 2016
- Adding a table of unit square normalization scales.
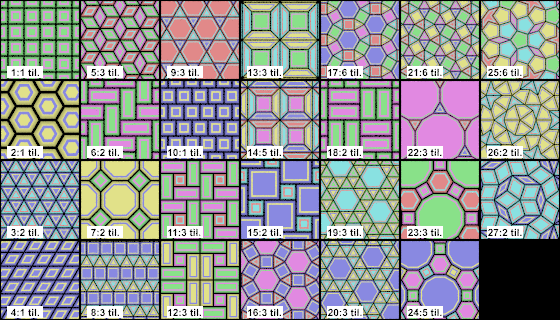
The tiling pattern creates a series tiles in the x-z plane. See the image below for examples of the twenty-seven available patterns.
The syntax is as follows:
pigment {
tiling Pattern_Number
[PATTERN_MODIFIERS...]
}
The various tiling patterns annotated by tiling pattern and tiling type respectively |
For each pattern, each individual tile of the pattern has the same beveling as the other tiles in that pattern, allowing regular caulking to be defined. For a pattern with N tile types (where N is the tiling type noted in the above image) the main color/texture of the tiles are at x/N with x going from 0 to N-1, and the extreme color/texture caulk for these tiles are at (x+1)/N. The bevel covers the range between these two values.
To begin exploring the tiling pattern right away, see the distribution file ~scenes/textures/pattern/tiling.pov. It uses obvious colors to better illustrate how the feature works, and you can optionally write it's color_map to a text file. Once you get a feel for the break points, you can always define you own map!
The scale required to fit the core repeated tile into a unit square size for each tiling pattern is given in the table below.
| Tiling Number | Unit square normalization scale |
|---|---|
| 1 | <1,1,1> |
| 2 | <2/3,1,1/sqrt(3)> |
| 3 | <1,1,2/sqrt(3)> |
| 4 | <1,1,2/sqrt(3)> |
| 5 | <2/3,1,1/sqrt(3)> |
| 6 | <1/4,1,1/4> |
| 7 | <1/(sqrt(2)+1),1,1/(sqrt(2)+1)> |
| 8 | <1,1,1/(sqrt(3)+2)> |
| 9 | <1/2,1,1/(2*sqrt(3))> |
| 10 | <1,1,1/2> |
| 11 | <1/3,1,1/3> |
| 12 | <1/3,1,1/3> |
| 13 | <1/(sqrt(3)+1),1,1/(sqrt(3)+1)> |
| 14 | <1/(sqrt(3)+1),1,1/(sqrt(3)+1)> |
| 15 | <1/5,1,1/5> |
| 16 | <1/(sqrt(3)+3),1,1/((sqrt(3)+1.0)*2.0)> |
| 17 | <1/(sqrt(3)+3),1,1/((sqrt(3)+1.0)*2.0)> |
| 18 | <1/4,1,1/4> |
| 19 | <1/2,1,1/((sqrt(3)/2)*3)> |
| 20 | <1/2,1,1/((sqrt(3)/2)*3)> |
| 21 | <1/(1+sqrt(3)),1,1/(1+sqrt(3))> |
| 22 | <1/(2+sqrt(3)),1,1/(3+(2*sqrt(3)))> |
| 23 | <1/(3+sqrt(3)),1,1/(3+(3*sqrt(3)))> |
| 24 | <1/(3+sqrt(3)),1,1/(3+(3*sqrt(3)))> |
| 25 | <1/(4*sqrt(2)),1,1/(4*sqrt(2))> (*) |
| 26 | <1/(4*sqrt(2)),1,1/(4*sqrt(2))> (*) |
| 27 | <1/(4*sqrt(2)),1,1/(4*sqrt(2))> (*) |
(*) - Unit square scaling not possible with penrose tiling. Scaling given useful to see all tiles in a way symmetrical in z. |
|