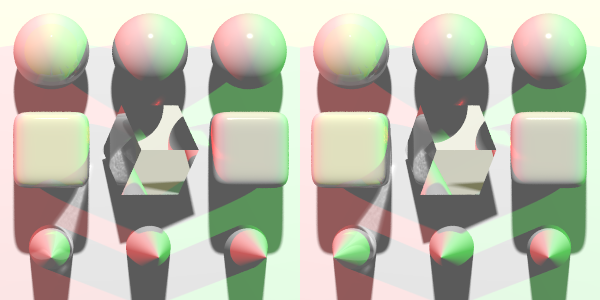User:Le Forgeron/cameras

From POV-Wiki
Jump to navigation Jump to search

Access to camera information

These pieces of information are in read-only mode. You cannot use them to modify the actual value (no #declare or #local). The various vectors might have been updated by transform and look_at.

  • camera_type is a string containing the type of the camera (but not its subtype, so cylinder camera might be ambiguous).
  • camera_up is the actual up vector of the camera.
  • camera_right is the actual right vector of the camera.
  • camera_direction is the actual direction vector of the camera.
  • camera_location is the actual location of the camera.

In case of scene with multiple cameras, each keyword can be followed by an usual array notation to access the relevant camera. (e.g. camera_up[3] for the fourth camera)

multiple cameras on the same image

grid

Multiple cameras on the same scene can be put in a grid which divides the rendered image in N horizontal and M vertical identical blocks. Filled from left to right, and from top to bottom, each block must have a declared camera (either as a `#declare` or `#local` identifier). 

camera { grid N CameraId\{N*N\} `}`
camera { grid <N,M> CameraId\{N*M\} }
#declare C2= camera {
  fisheye_orthographic 
  location <1,4,3> 
  right    x/3*image_width/image_height 
  angle 360 
  look_at <0,1,2> 
}
#declare C3= camera { 
  fisheye_equisolid_angle 
  location <1,4,3> 
  right    x/3*image_width/image_height
  angle 360 
  look_at <0,1,2> 
}
#declare C4= camera { 
  fisheye_stereographic 
  location <1,4,3> 
  right    x/3*image_width/image_height 
  angle 360 look_at <0,1,2> 
}

camera { grid <3,1> C2 C3 C4 }

#version 3.8;
global_settings{ assumed_gamma 1.0 }

#include "scene.inc"

#declare C=camera { right x };
#declare D=camera { disc C };
#declare E=camera { diamond C };
#declare F=camera { orthographic right 5*x up 5*y };
#declare G=camera { matte 0.1 0.1 C };
#declare H=camera { liner 0.1 0.1 F };

camera { grid <4,3> C D E F G H C E F D H G }
LeForgeronGrid.png

splitted in two, unregular

#version 3.8;
global_settings{ assumed_gamma 1.0 }

#include "scene.inc"

#declare C=camera { right image_width/image_height*x up y*4 };
#declare D=camera { right image_width/image_height*x*3 up y*4 angle 60};

camera { horizontal 0.25 C D  }
LeForgeronHorizontal.png
 
#version 3.8;
global_settings{ assumed_gamma 1.0 }

#include "scene.inc"

#declare C=camera { right image_width/image_height*x*4 };
#declare D=camera { right image_width/image_height*x*4/3 };

camera { vertical 0.25 C D  }
240px

other fisheye camera

The historical fisheye in povray is for r = F.theta. It is equidistant (linear scaled). It maintains angular distances.

  • fisheye_orthographic for r = F.sin(theta). It is orthographic. It maintains planar illuminance.
  • fisheye_equisolid_angle for r = F.2.sin(theta/2). It is equisolid angle (equal area). It maintains surface relations.
  • fisheye_stereographic for r = F.2.tan(theta/2). It is stereographic (conform). It maintains angles.

other fisheye cameras

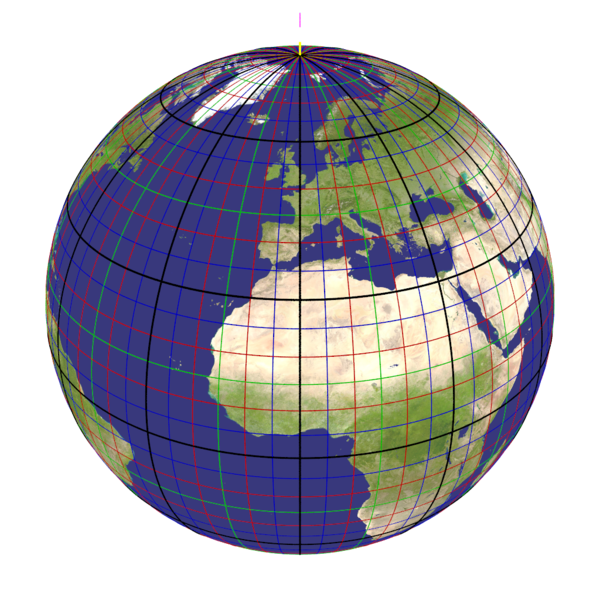
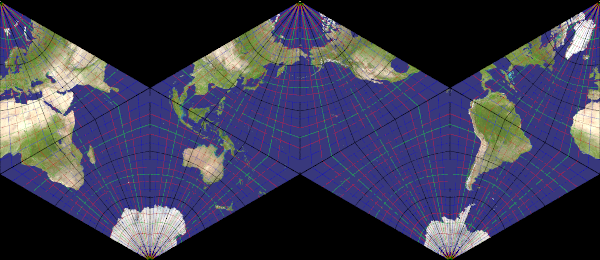
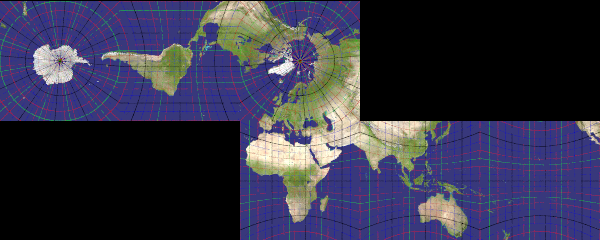
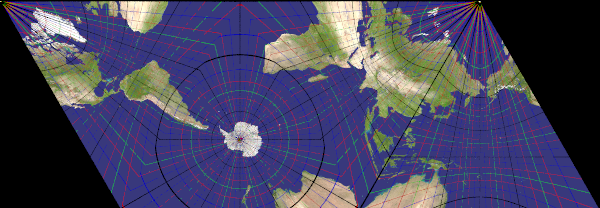
Cartographic Camera

You knew orthographic, ultra_wide_angle, spherical, omnimax, fisheye, perspective and others, here a few new kinds.

The recommendation about the ratio is for the the final picture's dimensions, assuming square pixels.

Put the location above the intended center, in orbit. The location+direction should provide the center of the planet.

LeForgeronCamera perspective.png

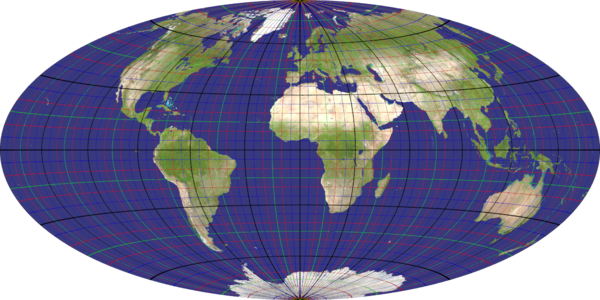
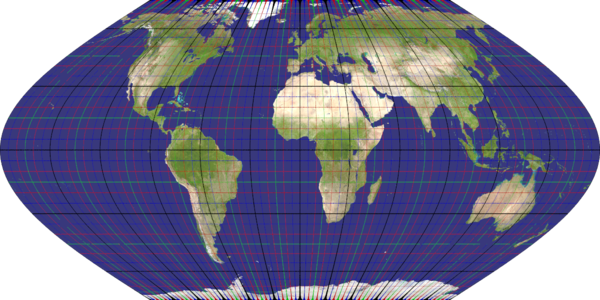
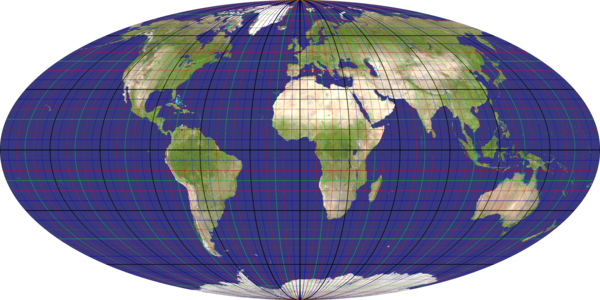
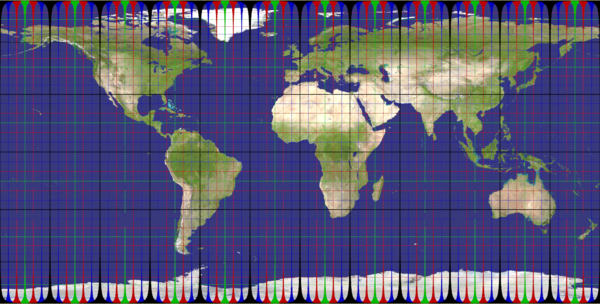
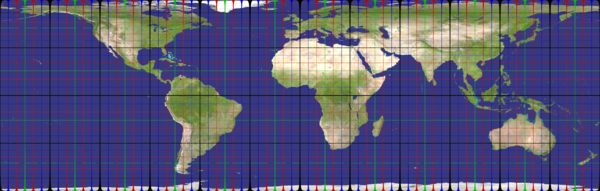
aitoff_hammer

Recommended ratio is 2:1

LeForgeronCamera aitoff hammer.png

eckert_iv

Recommended ratio is 2:1

LeForgeronCamera eckert iv.png

eckert_vi

Recommended ratio is 2:1

LeForgeronCamera eckert vi.png

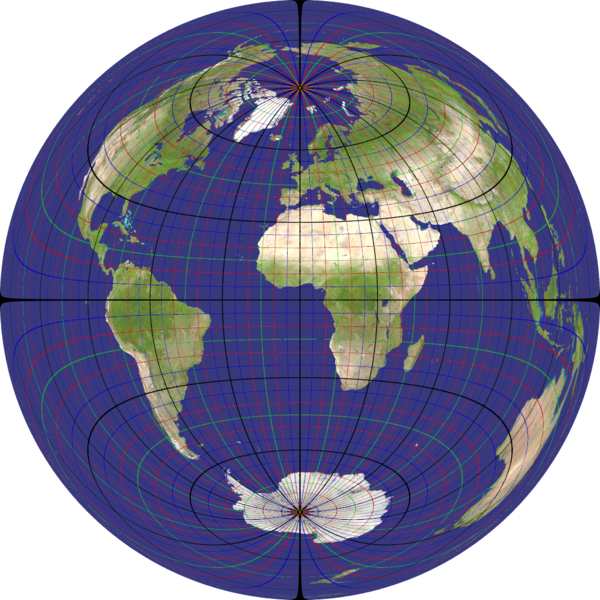
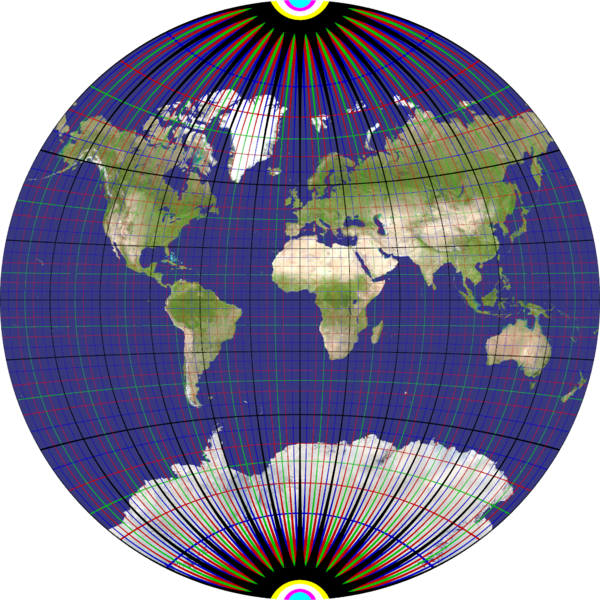
lambert_azimuthal

Recommended ratio is 1:1

LeForgeronCamera lambertazi.png

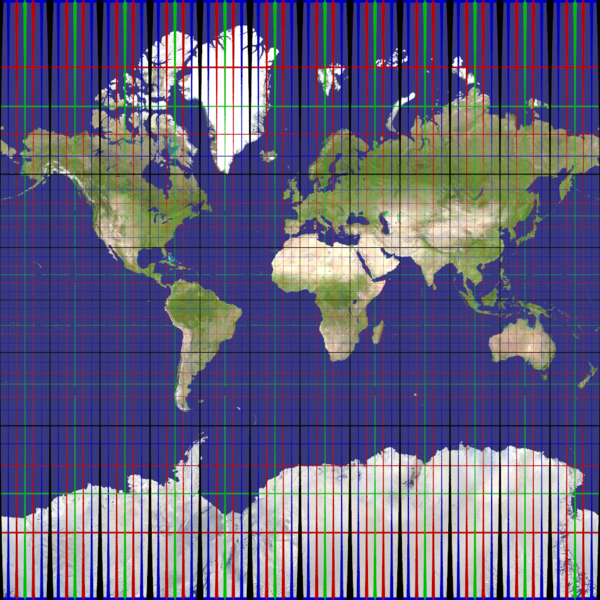
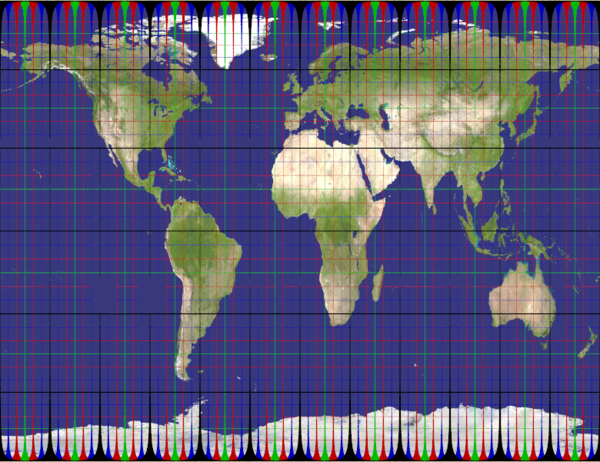
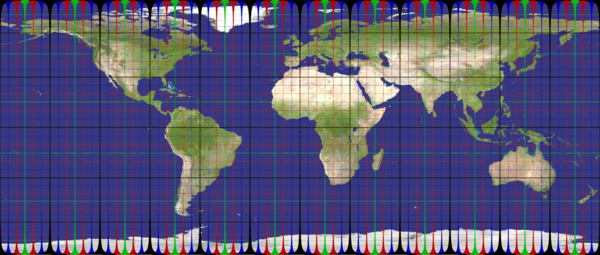
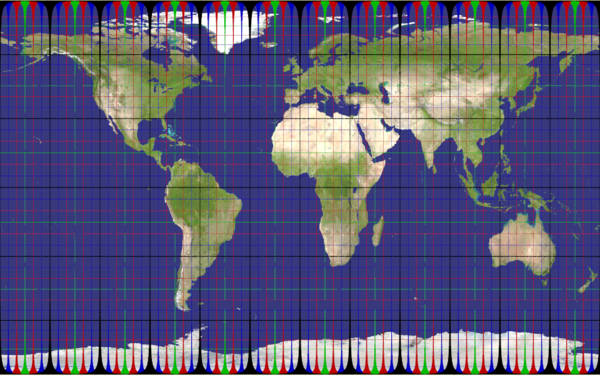
mercator

Recommended ratio is up to you, as you need a very large height/wide to hope reaching the poles (nah, it's impossible with that projection).

LeForgeronCamera mercat.png

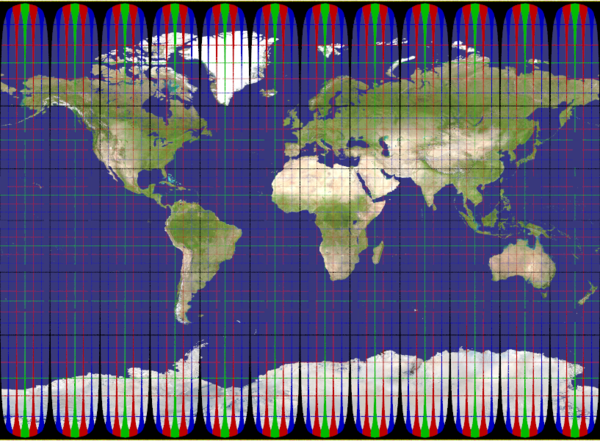
miller_cylindrical

Recommended ratio is 1.3638862 or 1:0.733

LeForgeronCamera miller.png

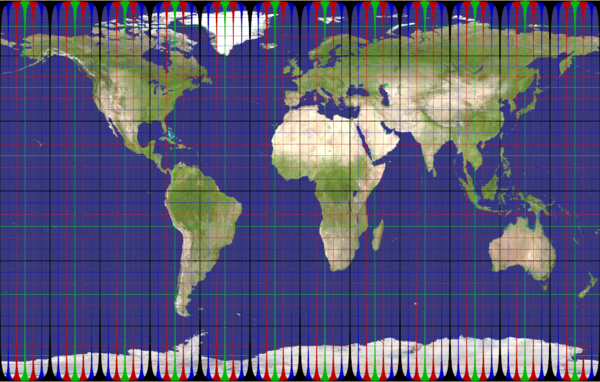
mollweide

Recommended ratio is 2:1

LeForgeronCamera mollweide.png

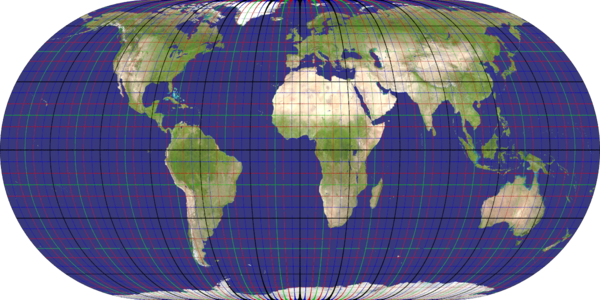
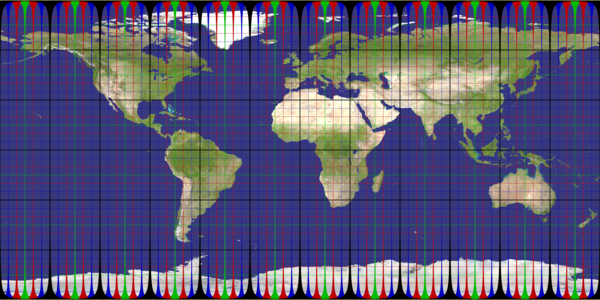
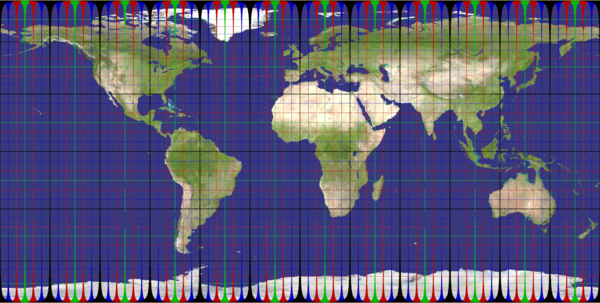
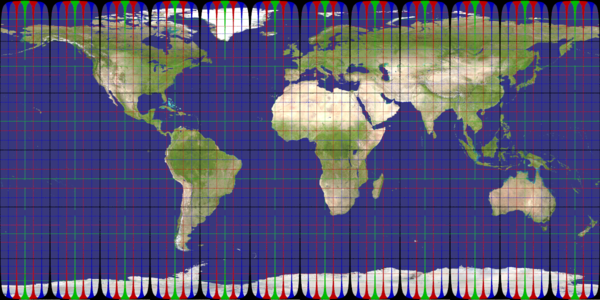
plate_carree

Recommended ratio is 2:1

LeForgeronCamera platecarree.png

van_der_grinten

Recommended ratio is 1:1

LeForgeronCamera van der grinten.png


Cylindrical Equal Area Projection

formula for ratio is π.cos²(φ) with φ the standard parallel.

balthasart

Recommended ratio is about 1.3.

The standard parallel of the projection is 50°.

LeForgeronCamera balthasart.png

behrmann

Recommended ratio is 3π:4 (about 2.36)

The standard parallel of the projection is 30°.

LeForgeronCamera behrmann.png

edwards

Recommended ratio is about 2.

The standard parallel of the projection is 37°24'.

LeForgeronCamera edwards.png

gall

Recommended ratio is π:2 or golden ratio (φ) (both near 1.6).

The standard parallel of the projection is 45°.

LeForgeronCamera gall.png

hobo_dyer

Recommended ratio is about 2.

The standard parallel of the projection is 37°30'.

LeForgeronCamera hobo dyer.png

lambert_cylindrical

Recommended ratio is π

The standard parallel of the projection is 0°.

LeForgeronCamera lambertcyl.png

peters

Recommended ratio is about π:2 or golden ratio φ (not exactly the same thing, but around 1.6).

The standard parallel of the projection is 44.138°.

LeForgeronCamera peters.png

smyth_craster

Recommended ratio is about 2.

The standard parallel of the projection is 37°04'.

LeForgeronCamera smyth craster.png

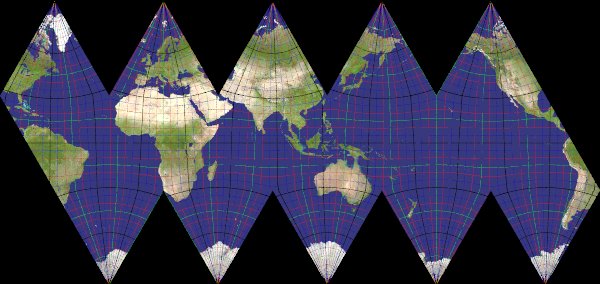
Unfolding platonic

Of the 5 platonic solids, 4 are easy to unfold to make a map. The dodecahedron is not available so far.

icosa

Recommended ratio is about 2.1169 ( 11.sqrt(3):9 )

LeForgeronCamera icosa.png

octa

Recommended ratio is about 2.3 ( 4:sqrt(3) )

LeForgeronCamera octa.png

cube

Recommended ratio is 2.5 ( 5:2 )

LeForgeronCamera cube.png


tetra

Recommended ratio is about 2.886 ( 5:sqrt(3) )

LeForgeronCamera tetra.png

Camera for 3D

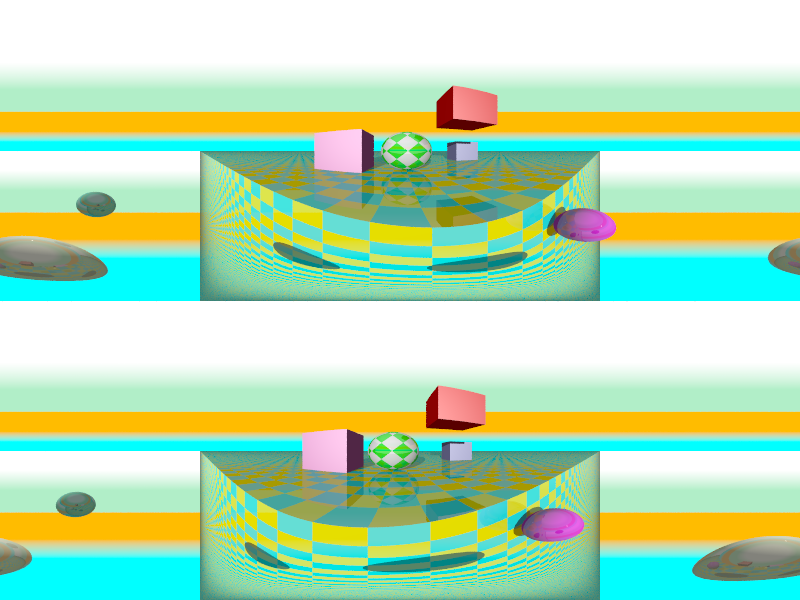
Stereoscopic camera

The right's length is adjusted automatically to take into account that there is two images. Just use the same right you would with a picture of half the width. Or think of it the other way : the view is HxW, the rendering is to be done for a Hx(2W). 

camera
{ stereo distance (clock <0 ? -26:26 )
  parallaxe atan2(13*clock,300)
 location -300*z
 right image_width/image_height*x
 direction z
 up y
 angle 15
 }

LeForgeronStereoCrossed.png

cross-eyed viewing:
distance is negative

LeForgeronStereoFocus.png

Parallel viewing:
distance is positive

LeForgeronStereoParallel.png

Parallel viewing with 0 parallaxe
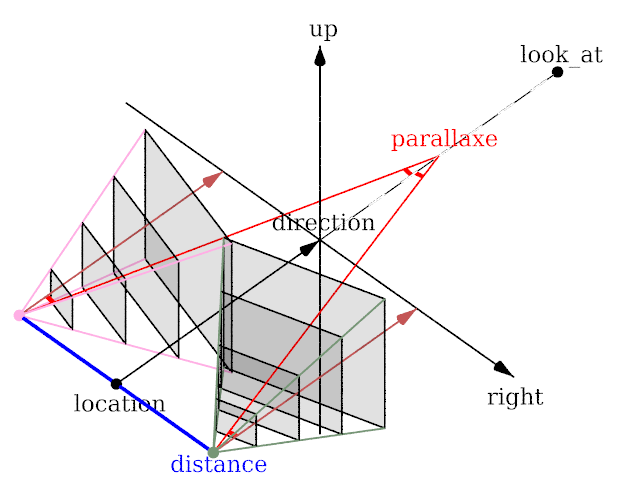
  • distance provides the distance, along the right axis's direction, between the eyes. The location of the camera is the middle point.
    • use a positive value for parallel viewing
    • use a negative value for cross-eyed viewing
    • default is 0
  • parallaxe is the angle between the eyes's direction:
    • should normally be of the same sign of distance
    • normal value is atan2( half distance value, distance to focus )
    • default is 0

RefImgCameraViewStereo.png

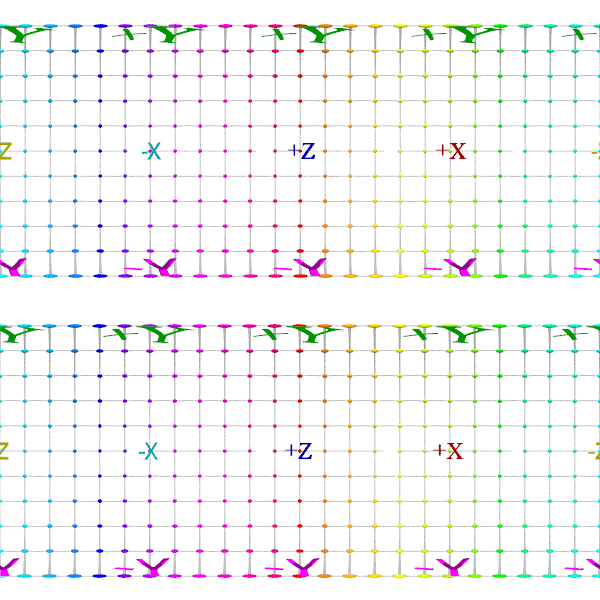
Omni Directional Stereo camera

camera
{ omni_directional_stereo 
  distance 1
  location 0
  up 10*y
  right 10*x
  direction 10*z
}

The left eye is on top, and the right eye is of course the lower part.

"Omni Directional Stereo, ODS"


LeForgeronODS.png

ODS picture
  • distance provides the distance, along the right axis's direction, between the eyes. The location of the camera is the middle point.
Retrieved from "https://wiki.povray.org/content?title=User:Le_Forgeron/cameras&oldid=10505"