Difference between revisions of "Documentation:Tutorial Section 3.3"
m (→Using Ambient: canonicalize a version number) |
m (→Gamma in Legacy Scenes: canonicalize some version numbers) |
||
| Line 453: | Line 453: | ||
<ul> | <ul> | ||
| − | <li>If the scene contains an <code>assumed_gamma</code> statement, and does not explicitly specify a version of | + | <li>If the scene contains an <code>assumed_gamma</code> statement, and does not explicitly specify a version of v3.7 or later, gamma handling will follow the v3.6 rules.</li> |
| − | <li>If the scene does neither specify an <code>assumed_gamma</code> statement, nor explicitly specify a version of | + | <li>If the scene does neither specify an <code>assumed_gamma</code> statement, nor explicitly specify a version of v3.7 or later, gamma correction will be turned off.</li> |
</ul> | </ul> | ||
| − | <p>The | + | <p>The v3.6 rules differ from standard behaviour with regards to <code>image_map</code> input files as follows:</p> |
<ul> | <ul> | ||
<li>For OpenEXR, Radiance HDR and PNG, the behaviour is the same as described above.</li> | <li>For OpenEXR, Radiance HDR and PNG, the behaviour is the same as described above.</li> | ||
| − | <li>For any other file formats, in " | + | <li>For any other file formats, in "v3.6 mode" POV-Ray will currently presume the image data to match the <code>assumed_gamma</code> (in other words, no gamma adjustment will be performed by default).</li> |
</ul> | </ul> | ||
| − | <p>As POV-Ray | + | <p>As POV-Ray v3.6 did not have a File_Gamma setting, and used Display_Gamma for both purposes, you will have to set File_Gamma to whatever you used to set Display_Gamma to (or leave it undefined if you did not specify Display_Gamma either) in order to get the same output.</p> |
| − | <p>Furthermore, backward compatibility with | + | <p>Furthermore, backward compatibility with v3.6 for PNG input files is subject to the following restrictions:</p> |
<ul> | <ul> | ||
<li>For palette-based PNG files (an uncommon flavor of PNG), backward compatibility is provided only if gamma correction is disabled (i.e. <code>assumed_gamma</code> is <em>not</em> specified). This is due to fixes in the handling of this PNG flavor.</li> | <li>For palette-based PNG files (an uncommon flavor of PNG), backward compatibility is provided only if gamma correction is disabled (i.e. <code>assumed_gamma</code> is <em>not</em> specified). This is due to fixes in the handling of this PNG flavor.</li> | ||
| − | <li>For non-palette-based PNG files, backward compatibility is provided only if gamma correction is enabled (i.e. <code>assumed_gamma</code> <em>is</em> specified). This is due to inconsistencies in POV-Ray | + | <li>For non-palette-based PNG files, backward compatibility is provided only if gamma correction is enabled (i.e. <code>assumed_gamma</code> <em>is</em> specified). This is due to inconsistencies in POV-Ray v3.6's PNG file handling which would have been prohibitively difficult to reproduce with the architectural changes in POV-Ray v3.7.</li> |
| − | <li>For PNG files carrying both an sRGB chunk and a fitting gAMA chunk, results will slightly differ, while for PNG files carrying an sRGB chunk but no gAMA chunk (or a wrong one), backward compatibility is not provided. This is due to POV-Ray | + | <li>For PNG files carrying both an sRGB chunk and a fitting gAMA chunk, results will slightly differ, while for PNG files carrying an sRGB chunk but no gAMA chunk (or a wrong one), backward compatibility is not provided. This is due to POV-Ray v3.6 honoring only gAMA chunks, while POV-Ray v3.7 honors sRGB chunks as well, giving them precedence over gAMA chunks to comply with the official file format specification.</li> |
</ul> | </ul> | ||
| − | <p>If you experience problems with a PNG input file in a legacy scene, explicitly specify the decoding gamma to be applied for that particular image using the <code>gamma</code> statement may help. When using e.g. <code>assumed gamma 1.8</code>, some values worth trying would be <code>gamma 1</code>, <code>gamma 1/1.8</code>, <code>gamma 2.2/1.8</code> or <code>gamma 1.8</code>. (With POV-Ray | + | <p>If you experience problems with a PNG input file in a legacy scene, explicitly specify the decoding gamma to be applied for that particular image using the <code>gamma</code> statement may help. When using e.g. <code>assumed gamma 1.8</code>, some values worth trying would be <code>gamma 1</code>, <code>gamma 1/1.8</code>, <code>gamma 2.2/1.8</code> or <code>gamma 1.8</code>. (With POV-Ray v3.6's PNG file handling having been quite a mess, it is difficult to be more specific.)</p> |
===Advanced Texture Options=== | ===Advanced Texture Options=== | ||
Revision as of 15:20, 9 June 2021
|
This document is protected, so submissions, corrections and discussions should be held on this documents talk page. |
Other Shapes
Superquadric Ellipsoid Object
Sometimes we want to make an object that does not have perfectly sharp
edges like a box does. Then, the superquadric ellipsoid shape made by the
superellipsoid is a useful object. It is described by the simple
syntax:
superellipsoid { <Value_E, Value_N >}
Where Value_E and Value_N are float values greater than
zero and less than or equal to one. Let's make a superellipsoid and
experiment with the values of Value_E and Value_N to see
what kind of shapes we can make. We create a file called
supellps.pov and edit it as follows:
#include "colors.inc"
camera {
location <10, 5, -20>
look_at 0
angle 15
}
background { color rgb <.5, .5, .5> }
light_source { <10, 50, -100> White }
The addition of a gray background makes it a little easier to see our object. We now type:
superellipsoid { <.25, .25>
pigment { Red }
}
We save the file and render it to see the shape. It will look like a box, but the edges will be rounded off. Now let's experiment with different values of Value_E and Value_N. For the next trace, try <1, 0.2>. The shape now looks like a cylinder, but the top edges are rounded. Now try <0.1, 1>. This shape is an odd one! We do not know exactly what to call it, but it is interesting. Finally, let's try <1, 1>. Well, this is more familiar... a sphere!
There are a couple of facts about superellipsoids we should know. First, we should not use a value of 0 for either Value_E nor Value_N. This will cause POV-Ray to incorrectly make a black box instead of our desired shape. Second, very small values of Value_E and Value_N may yield strange results so they should be avoided. Finally, the Sturmian root solver will not work with superellipsoids.
Superellipsoids are finite objects so they respond to auto-bounding and can be used in CSG.
Now let's use the superellipsoid to make something that would be useful in a scene. We will make a tiled floor and place a couple of superellipsoid objects hovering over it. We can start with the file we have already made.
We rename it to tiles.pov and edit it so that it reads as
follows:
#include "colors.inc"
#include "textures.inc"
camera {
location <10, 5, -20>
look_at 0
angle 15
}
background { color rgb <.5, .5, .5> }
light_source{ <10, 50, -100> White }
Note: We have added #include "textures.inc" so
we can use pre-defined textures. Now we want to define the superellipsoid
which will be our tile.
#declare Tile = superellipsoid { <0.5, 0.1>
scale <1, .05, 1>
}
Superellipsoids are roughly 2*2*2 units unless we scale them otherwise. If we wish to lay a bunch of our tiles side by side, they will have to be offset from each other so they do not overlap. We should select an offset value that is slightly more than 2 so that we have some space between the tiles to fill with grout. So we now add this:
#declare Offset = 2.1;
We now want to lay down a row of tiles. Each tile will be offset from the
original by an ever-increasing amount in both the +z and -z directions. We
refer to our offset and multiply by the tile's rank to determine the
position of each tile in the row. We also union these tiles into a single
object called Row like this:
#declare Row = union {
object { Tile }
object { Tile translate z*Offset }
object { Tile translate z*Offset*2 }
object { Tile translate z*Offset*3 }
object { Tile translate z*Offset*4 }
object { Tile translate z*Offset*5 }
object { Tile translate z*Offset*6 }
object { Tile translate z*Offset*7 }
object { Tile translate z*Offset*8 }
object { Tile translate z*Offset*9 }
object { Tile translate z*Offset*10 }
object { Tile translate -z*Offset }
object { Tile translate -z*Offset*2 }
object { Tile translate -z*Offset*3 }
object { Tile translate -z*Offset*4 }
object { Tile translate -z*Offset*5 }
object { Tile translate -z*Offset*6 }
}
This gives us a single row of 17 tiles, more than enough to fill the
screen. Now we must make copies of the Row and translate them,
again by the offset value, in both the +x and -x directions in ever
increasing amounts in the same manner.
object { Row }
object { Row translate x*Offset }
object { Row translate x*Offset*2 }
object { Row translate x*Offset*3 }
object { Row translate x*Offset*4 }
object { Row translate x*Offset*5 }
object { Row translate x*Offset*6 }
object { Row translate x*Offset*7 }
object { Row translate -x*Offset }
object { Row translate -x*Offset*2 }
object { Row translate -x*Offset*3 }
object { Row translate -x*Offset*4 }
object { Row translate -x*Offset*5 }
object { Row translate -x*Offset*6 }
object { Row translate -x*Offset*7 }
Finally, our tiles are complete. But we need a texture for them. To do
this we union all of the Rows together and apply a White
Marble pigment and a somewhat shiny reflective surface to it:
union{
object { Row }
object { Row translate x*Offset }
object { Row translate x*Offset*2 }
object { Row translate x*Offset*3 }
object { Row translate x*Offset*4 }
object { Row translate x*Offset*5 }
object { Row translate x*Offset*6 }
object { Row translate x*Offset*7 }
object { Row translate -x*Offset }
object { Row translate -x*Offset*2 }
object { Row translate -x*Offset*3 }
object { Row translate -x*Offset*4 }
object { Row translate -x*Offset*5 }
object { Row translate -x*Offset*6 }
object { Row translate -x*Offset*7 }
pigment { White_Marble }
finish { phong 1 phong_size 50 reflection .35 }
}
We now need to add the grout. This can simply be a white plane. We have stepped up the ambient here a little so it looks whiter.
plane {
y, 0 //this is the grout
pigment { color White }
finish { ambient .4 diffuse .7 }
}
To complete our scene, let's add five different superellipsoids, each a different color, so that they hover over our tiles and are reflected in them.
superellipsoid {
<0.1, 1>
pigment { Red }
translate <5, 3, 0>
scale .45
}
superellipsoid {
<1, 0.25>
pigment { Blue }
translate <-5, 3, 0>
scale .45
}
superellipsoid {
<0.2, 0.6>
pigment { Green }
translate <0, 3, 5>
scale .45
}
superellipsoid {
<0.25, 0.25>
pigment { Yellow }
translate <0, 3, -5>
scale .45
}
superellipsoid {
<1, 1>
pigment { Pink }
translate y*3
scale .45
}
|
Some superellipsoids hovering above a tiled floor. |
We trace the scene at 320x200 -A to see the result. If we are
happy with that, we do a final trace at 640x480 +A0.2.
Gamma Handling
In this section, we will explain how to use the gamma handling framework introduced with POV-Ray version 3.7. However, first we may need to introduce the term gamma, and why it needs handling anyway:
Note: In a nutshell, gamma handling is the compensation for non-linearities in the representation of color values.
|
As a raytracing engine, POV-Ray internally needs to represent colors using linear light intensity values to produce physically accurate results. However, the majority of contemporary digital image processing tools and file formats do not. This comes as a surprise to most people, probably because the human visual perception is non-linear as well, as can be demonstrated in the render to the right, generated with POV-Ray using physically realistic settings: |
|
|
gamma handling reference image |
Both front and second row show spheres with pigments increasing from rgb 0.0 to rgb 1.0. When asked which of them increases linearly, with a medium grey at the center, most people will go for the front row without too much hesitation. And in fact the pigment of the front center sphere does correspond to what Photoshop or similar image processing software would normally call 50% grey, but as a matter of fact it reflects only 21.8% as much light as the rightmost one. The sphere truly reflecting 50% as much light sits right behind it.
A corresponding nonlinearity can be found in the traditional internal representation of colors in digital image processing, as implemented in file formats, graphics cards frame buffers, display APIs and so forth. Using one byte per colour component, and black and white represented by (0;0;0) and (255;255;255) respectively, a value of (128;128;128) will typically be used to encode a light intensity of just about 20%. To make matters a bit more complicated, the actual light intensity seen on the computer display may vary from one computer to the next, not only due to a historical lack of standardization in the PC display and graphics hardware market, but also due to factors such as electrical tolerances and even aging of the display. In professional environments, displays are therefore calibrated at regular intervals.
The non-linear relationship between color values and actual light intensity is usually approximated by (or calibrated to match) a power-law function (aka gamma function, hence the technical term gamma), i.e.:
f(x) = x ̂ γ
where x is the internal representation normalized to the range [0...1], f(x) is the actual output light intensity, and γ is a value typically somewhere between 2.0 to 2.4, though in the professional image processing world a value of 1.8 is also common.
Another formula becoming more and more popular is the so-called sRGB transfer function as defined in the sRGB color space standard, which has been adopted as the official standard on the World Wide Web. This function roughly corresponds to a power-law gamma of 2.2. Other standard transfer functions worth mentioning are those defined by the TV broadcasting standards ITU-R BT.709 and ITU-R BT.2020.
Setting Up Your Display
Using POV-Ray's gamma handling framework will not make much sense unless your display is set up properly; ideally, this would be done with a colorimeter and professional display calibration software. However, for hobbyists' purposes, less expensive solutions will suffice:
- Your graphics card drivers may come with a wizard to help you adjust your display.
- Various versions of Photoshop shipped with a utility called "Adobe Gamma".
- There are numerous sites on the internet dedicated to getting your display settings straight.
Note: We disagree with the author of the site linked to above, about which display gamma to aim for, and strongly recommend a gamma of 2.2, unless you know exactly what you're doing.
As an additional sanity check of your system display settings (and also of your image viewing software) POV-Ray provides a sample scene custom-tailored to this purpose. Just render ~scenes/output/gamma_showcase.pov twice, using the following options:
+w640 +h480 +a0.3 +am1 +fN -d File_Gamma=sRGB Output_File_Name=gamma_showcase.png +w640 +h480 +a0.3 +am1 +fN -d File_Gamma=1.0 Output_File_Name=gamma_showcase_linear.png
At 100% zoom, both images should look identical in your viewing software (if they don't, then by all means get rid of that obsolete software). Moreover, all the spheres should look uniform, like in the introductory image above. It is ok if you notice stripes on the spheres, but the overall brightness and hue should not be perceived as varying between the left and right hemispheres of any single sphere.
If however the image appears like shown below, then your system display gamma is either higher (left) or lower (right) than what your image viewing software expects. Note that in the PC world, most contemporary software will expect the display to either have a gamma of 2.2 or comply with the sRGB transfer function, unless there's a way to tell the software otherwise.
Note: Make sure to set your desktop resolution to match the native resolution of your display, as interpolation might mess up the intended effect. Also, some types of displays exhibit variations of gamma depending on viewing angle and, as a result, also across the display area; in that case, we recommend to adjust your display so that you get the desired gamma at the center of the screen when sitting as you usually do.
|
higher example |
lower example |
Just for the sake of it, here's a render of that showcase scene (note however that due to conversion of the original documentation source to whatever format you are currently reading it in, whether it be PDF, HTML or whatever, the image may have undergone some conversion, and may therefore be unsuited to serve as a good reference):
|
refer to: scenes/gamma/gamma_showcase.pov |
Setting Up POV-Ray
Now that you can be sure that your operating system in general and your image viewing software in particular behave well regarding gamma, it is time to set up POV-Ray to do the same.
If you know that your system matches the sRGB standard, or have chosen to go for an approximate display gamma of 2.2, or used a tool that doesn't explicitly mention the gamma it has helped you to set up (in which case it will typically be 2.2 or sRGB as well), you're probably done already, as POV-Ray expects sRGB compliance by default, which is close enough to a display gamma of 2.2 for starters. Otherwise (or if you want an exact display gamma of 2.2) you should edit your master povray.ini to add the following line (e.g. for a display gamma of 1.8):
Display_Gamma=1.8
Instead of a numerical value, you can also specify Display_Gamma=sRGB to explicitly tell POV-Ray that your system is calibrated to match the sRGB standard (which, as already mentioned, is actually the default setting). New in version 3.8, you can also specify Display_Gamma=BT709 or Display_Gamma=BT2020 to explicitly tell POV-Ray that your system is calibrated to match the transfer functions specified in ITU-R BT.709 or BT.2020, respectively, but you shouldn't use these unless you absolutely know what you are doing.
Again, the gamma showcase scene can be used as a sanity check; use the following parameters:
+w640 +h480 +a0.3 +am1 -f +d
Make sure you set the preview to windowed mode to get a 100% zoom. If everything works as expected, the preview window should look just like the PNG files already created, with each sphere again appearing to have a uniform color and brightness. If this is not the case for some mysterious reason, you may need to tweak the Display_Gamma setting accordingly; increase it if the left hemispheres appear too dark, or decrease it if they appear too bright. When you're done testing, update your povray.ini again.
Gamma in Output Images
Besides being used internally in most contemporary digital image processing software, non-linear color representations are also used in most conventional image file formats. This is often called gamma pre-correction, in the sense that the original linear light intensity information has already been transformed by a gamma function to compensate for display non-linearity. Unfortunately, due to the large variety of display gamma in the world of computing, the gamma value used for pre-correction traditionally followed no set standard either.
In recent years the situation has changed, partly due to the adoption of the sRGB standard as the official recommendation for the World Wide Web, with major file format specifications following suit, and partly due to the advent of new file formats like PNG designed right from the start for a standardized way of gamma handling. (For such file formats, it is customary to speak of non-linear color representation not as gamma pre-correction, but rather as gamma encoding.) By now, for virtually all contemporary file formats there exists either a clear specification of how to handle gamma, or an official recommendation to adhere to the sRGB standard.
POV-Ray's gamma handling defaults are set to comply with the official file format standards or recommendations, so normally you will not need to worry about gamma handling. However, should the need arise, you can tell POV-Ray to ignore gamma recommendations and pre-correct the output file for a different display gamma, using the File_Gamma INI file option, e.g.:
File_Gamma=1.8
Again, sRGB as well as, New in version 3.8, BT709 or BT2020, are valid values, specifying that POV-Ray should apply the sRGB, ITU-R BT.709 or BT.2020 transfer function, respectively.
Note: Some of the file formats supported by POV-Ray are explicitly specified to never use gamma pre-correction or gamma encoding. For such file types (currently OpenEXR and Radiance HDR), File_Gamma has no effect whatsoever. For certain other file types (currently PNG), File_Gamma does have an effect on the encoding of the image, but not on the general visual appearance.
For output files, POV-Ray handles gamma according to the following rules:
- For OpenEXR and Radiance HDR, which are officially specified to store linear light intensity values, POV-Ray always stores linear values, ignoring the
File_Gammasetting. - For PNG, which explicitly allows different encoding gamma values, POV-Ray will interpret the
File_Gammasetting as the decoding gamma to encode for, and always write corresponding metadata into the header; as a result, the image will always look virtually identical irregardless of theFile_Gammasetting; however, to minimize visible encoding artifacts like color banding, it is strongly recommended to use a setting of around 2.2, orsRGB. IfFile_Gammais not specified, PNG output defaults tosRGB. New in version 3.8, note that a setting ofBT709orBT2020is possible, but cannot be conveyed correctly via PNG metadata and is therefore strongly discouraged for this file format. - New in version 3.8, for Netpbm PPM, which is officially specified to store gamma-encoded values using the ITU-R BT.709 transfer function, POV-Ray adheres to the Netpbm standard by default. However, if the
File_Gammasetting is specified, POV-Ray will interpret it as a display gamma to pre-correct for, to account for the widespread use of competing de-facto standards, most notably the use of linear encoding (corresponding to a setting ofFile_Gamma=1.0) or sRGB gamma pre-correction (corresponding to a setting ofFile_Gamma=sRGB). - For all other file formats, POV-Ray will interpret the
File_Gammasetting as the display gamma to pre-correct for; as a result, the image will look different depending on the value used. It will also look different than the preview if you use a value other than your system's display gamma. IfFile_Gammais not specified, these output file formats default to sRGB pre-correction.
Setting Up Your Scene
As stated above, POV-Ray needs to work with linear colors to produce the most physically accurate output. However, if you prefer you can coax POV-Ray to work directly with non-linear color values. This is controlled via the assumed_gamma statement in the scene file's global settings, e.g.:
global_settings { assumed_gamma 1.8 }
This instructs POV-Ray to work with colors pre-corrected for a display gamma of whatever value you specify (in this example obviously a gamma of 1.8). You can also specify srgb instead of a numerical value, instructing POV-Ray to work with colors pre-corrected according to the sRGB standard. New in version 3.8, you can also specify bt709 or bt2020, but both are strongly discouraged.
Note: It is highly recommended to either set assumed_gamma to your system's display gamma for convenience, or set it to 1.0 for maximum realism. Using it for purely artistic purposes is strongly discouraged.
POV-Ray will take this setting into account when pre-correcting the computed image according to the Display_Gamma and File_Gamma settings.
Note: Sometimes you may want to use POV-Ray to generate other data than images in the strict sense, using the output image file as a mere data container, e.g. for height field data, bump maps, transparency maps or the like. In such cases, it is highly recommended to set both assumed_gamma and File_Gamma to 1.0 to avoid unexpected results.
Gamma in Literal Colors
By default, POV-Ray will expect each and every color value you enter to match your assumed_gamma, normalized to a range from 0.0 to 1.0. When using assumed_gamma 1.0 for realism, this can make it cumbersome to copy color values from other applications because those values will typically be non-linear representations of the respective colors; some people may also feel more at home with non-linear colors. To mitigate this issue, a special color literal syntax has been introduced to specify color values conforming to the sRGB standard; the syntax is as follows:
color srgb <Rp,Gp,Bp> color srgbf <Rp,Gp,Bp,F> color srgbt <Rp,Gp,Bp,T> color srgbft <Rp,Gp,Bp,F,T>
where Rp, Gp and Bp are pre-corrected color component values in the range from 0.0 to 1.0, while F and T are linear color component values in the same range.
Note: The filter and transmit components are always interpreted as linear values, and the use of this alternative syntax will have no effect on them.
The following is also valid and gives the expected results:
color srgb <255,240,0>/255
Note: This alternative syntax for colors does not constitute a new flavor of colors; instead, when encountering such a statement POV-Ray will immediately convert the specified non-linear color values into a linear ones. Any access to the individual components or computations done with the resulting color will therefore access the linear values.
Gamma in Input Images
Normally, gamma handling of input image files will work fine without intervention, but in some cases it may fail. To resolve such problems, the default handling can be overridden using the gamma SDL keyword, e.g:
image_map { jpeg "foo.jpg" gamma 1.8 }
Instead of a numerical value, you can also use the srgb keyword to inform POV-Ray that the file conforms to the sRGB standard. New in version 3.8, you can also specify bt709 or bt2020 to inform POV-Ray that the file is gamma-encoded using the ITU-R BT.709 or BT.2020 transfer functions, respectively
Note: Specifying gamma bt709 or gamma bt2020 only affects the transfer function used. Specifically, it does not affect the digital representation of nominal black and white, which remain at 0 and 255 (presuming 8-bit encoding), respectively, as opposed to 16 and 235 for full-fledged ITU-R BT-709 encoding.
For input files in general, the following rules apply:
- When using an image file in an
image_map, POV-Ray will always convert the image data to the scene'sassumed_gamma, according to whatever gamma the file is presumably pre-corrected for; you can override any file-specific presumtions by explicitly specifying thegammayou presume it to be pre-corrected for. - When using an image file in a
height_field,bump_maporimage_pattern, POV-Ray will convert the image data to linear values if you explicitly specify agammafor that particular file; if you don't, no gamma adjustment will be performed (or, in other words, the file will be presued to carry linear data, regardless of file format).
For image_map input files, the following file-specific rules apply:
- For OpenEXR and Radiance HDR, POV-Ray will presume the data to be linear, as per official file format specification.
- For PNG, POV-Ray will presume the image data to be encoded according to file header information (currently sRGB or gAMA chunks); in the absence of such information, POV-Ray will presume sRGB-compliant encoding as per official recommendation.
- For PPM and PGM, POV-Ray will currently presume the image data to match the
assumed_gamma(in other words, no gamma adjustment will be performed by default). New in version 3.8, POV-Ray will presume the image data to comply with the Netpbm specification, i.e. being gamma-encoded using the ITU-R BT.709 transfer function. - For any other file formats, POV-Ray will presume sRGB-compliant encoding, to match either official recommendations or common practice.
Note: If you explicitly specify gamma for a particular file, POV-Ray will ignore any file format specifications, recommendations or meta information, and always presume the file to be pre-corrected for the specified gamma, or encoded for the specified decoding gamma. This applies in all contexts and to all file formats without exception.
Gamma in Legacy Scenes
POV-Ray version 3.6 used slightly different rules for its (optional) gamma handling, while yet earlier versions used no gamma correction at all. To provide backward compatibility with legacy scenes, POV-Ray does its best to mimic the behavior of these older versions in the following cases:
- If the scene contains an
assumed_gammastatement, and does not explicitly specify a version of v3.7 or later, gamma handling will follow the v3.6 rules. - If the scene does neither specify an
assumed_gammastatement, nor explicitly specify a version of v3.7 or later, gamma correction will be turned off.
The v3.6 rules differ from standard behaviour with regards to image_map input files as follows:
- For OpenEXR, Radiance HDR and PNG, the behaviour is the same as described above.
- For any other file formats, in "v3.6 mode" POV-Ray will currently presume the image data to match the
assumed_gamma(in other words, no gamma adjustment will be performed by default).
As POV-Ray v3.6 did not have a File_Gamma setting, and used Display_Gamma for both purposes, you will have to set File_Gamma to whatever you used to set Display_Gamma to (or leave it undefined if you did not specify Display_Gamma either) in order to get the same output.
Furthermore, backward compatibility with v3.6 for PNG input files is subject to the following restrictions:
- For palette-based PNG files (an uncommon flavor of PNG), backward compatibility is provided only if gamma correction is disabled (i.e.
assumed_gammais not specified). This is due to fixes in the handling of this PNG flavor. - For non-palette-based PNG files, backward compatibility is provided only if gamma correction is enabled (i.e.
assumed_gammais specified). This is due to inconsistencies in POV-Ray v3.6's PNG file handling which would have been prohibitively difficult to reproduce with the architectural changes in POV-Ray v3.7. - For PNG files carrying both an sRGB chunk and a fitting gAMA chunk, results will slightly differ, while for PNG files carrying an sRGB chunk but no gAMA chunk (or a wrong one), backward compatibility is not provided. This is due to POV-Ray v3.6 honoring only gAMA chunks, while POV-Ray v3.7 honors sRGB chunks as well, giving them precedence over gAMA chunks to comply with the official file format specification.
If you experience problems with a PNG input file in a legacy scene, explicitly specify the decoding gamma to be applied for that particular image using the gamma statement may help. When using e.g. assumed gamma 1.8, some values worth trying would be gamma 1, gamma 1/1.8, gamma 2.2/1.8 or gamma 1.8. (With POV-Ray v3.6's PNG file handling having been quite a mess, it is difficult to be more specific.)
Advanced Texture Options
The extremely powerful texturing ability is one thing that really sets POV-Ray apart from other raytracers. So far we have not really tried anything too complex but by now we should be comfortable enough with the program's syntax to try some of the more advanced texture options.
Obviously, we cannot try them all. It would take a tutorial a lot more pages to use every texturing option available in POV-Ray. For this limited tutorial, we will content ourselves to just trying a few of them to give an idea of how textures are created. With a little practice, we will soon be creating beautiful textures of our own.
Note: Early versions of POV-Ray made a distinction between pigment and
normal patterns, i. e. patterns that could be used inside a
normal or pigment statement. Since POV-Ray 3.0 this
restriction was removed so that all patterns listed in section Pattern can be used as a pigment or normal pattern.
Pigments
Every surface must have a color. In POV-Ray this color is called a pigment. It does not have to be a single color. It can be a color pattern, a color list or even an image map. Pigments can also be layered one on top of the next so long as the uppermost layers are at least partially transparent so the ones beneath can show through. See also: Using Transparent Pigments and Layered Textures
Let's play around with some of these kinds of pigments.
We create a file called texdemo.pov and edit it as
follows:
#include "colors.inc"
camera {
location <1, 1, -7>
look_at 0
angle 36
}
light_source { <1000, 1000, -1000> White }
plane {
y, -1.5
pigment { checker Green, White }
}
sphere {
<0,0,0>, 1
pigment { Red }
}
Giving this file a quick test render we see that it is a simple red sphere against a green and white checkered plane. We will be using the sphere for our textures.
Using Color List Pigments
Before we begin we should note that we have already made one kind of
pigment, the color list pigment. In the previous example we have used a
checkered pattern on our plane. There are three other kinds of color list
pigments, brick, hexagon and the
object pattern.
Let's quickly try each of these. First, we change the plane's
pigment as follows:
pigment { hexagon Green, White, Yellow }
Rendering this we see a three-color hexagonal pattern. Note that this pattern requires three colors. Now we change the pigment to...
pigment { brick Gray75, Red rotate -90*x scale .25 }
Looking at the resulting image we see that the plane now has a brick pattern. We note that we had to rotate the pattern to make it appear correctly on the flat plane. This pattern normally is meant to be used on vertical surfaces. We also had to scale the pattern down a bit so we could see it more easily. We can play around with these color list pigments, change the colors, etc. until we get a floor that we like.
Using Pigment and Patterns
Let's begin texturing our sphere by using a pattern and a color map consisting of three colors. We replace the pigment block with the following.
pigment {
gradient x
color_map {
[0.00 color Red]
[0.33 color Blue]
[0.66 color Yellow]
[1.00 color Red]
}
}
Rendering this we see that the gradient pattern gives us an
interesting pattern of vertical stripes. We change the gradient direction to
y. The stripes are horizontal now. We change the gradient direction to z. The
stripes are now more like concentric rings. This is because the gradient
direction is directly away from the camera. We change the direction back to x
and add the following to the pigment block.
pigment {
gradient x
color_map {
[0.00 color Red]
[0.33 color Blue]
[0.66 color Yellow]
[1.00 color Red]
}
rotate -45*z // <- add this line
}
The vertical bars are now slanted at a 45 degree angle. All patterns can
be rotated, scaled and translated in this manner. Let's now try some
different types of patterns. One at a time, we substitute the following
keywords for gradient x and render to see the result: bozo,
marble, agate, granite,
leopard, spotted and wood
(if we like we can test all patterns listed in section Pattern).
Rendering these we see that each results in a slightly different pattern. But to get really good results each type of pattern requires the use of some pattern modifiers.
Using Pattern Modifiers
Let's take a look at some pattern modifiers. First, we change the pattern type to bozo. Then we add the following change.
pigment {
bozo
frequency 3 // <- add this line
color_map {
[0.00 color Red]
[0.33 color Blue]
[0.66 color Yellow]
[1.00 color Red]
}
rotate -45*z
}
The frequency modifier determines the number of times the
color map repeats itself per unit of size. This change makes the bozo
pattern we saw earlier have many more bands in it. Now we change
the pattern type to marble. When we rendered this earlier, we
saw a banded pattern similar to gradient y that really did not
look much like marble at all. This is because marble really is a kind of
gradient and it needs another pattern modifier to look like marble. This
modifier is called turbulence. We change the line
frequency 3 to turbulence 1 and render again. That's
better! Now let's put frequency 3 back in right after the
turbulence and take another look. Even more interesting!
But wait, it gets better! Turbulence itself has some modifiers of its own. We can adjust the turbulence several ways. First, the float that follows the turbulence keyword can be any value with higher values giving
us more turbulence. Second, we can use the keywords omega, lambda and octaves to change the turbulence parameters.
Let's try this now:
pigment {
marble
turbulence 0.5
lambda 1.5
omega 0.8
octaves 5
frequency 3
color_map {
[0.00 color Red]
[0.33 color Blue]
[0.66 color Yellow]
[1.00 color Red]
}
rotate 45*z
}
Rendering this we see that the turbulence has changed and the pattern looks different. We play around with the numerical values of turbulence, lambda, omega and octaves to see what they do.
Using Transparent Pigments and Layered Textures
Pigments are described by numerical values that give the rgb value of the color to be used (like color rgb<1,0,0> giving us a red
color). But this syntax will give us more than just the rgb values. We can
specify filtering transparency by changing it as follows: color
rgbf<1,0,0,1>. The f stands for filter,
POV-Ray's word for filtered transparency. A value of one means that the
color is completely transparent, but still filters the light according to
what the pigment is. In this case, the color will be a transparent red, like
red cellophane.
There is another kind of transparency in POV-Ray. It is called transmittance
or non-filtering transparency (the keyword is transmit;
see also rgbt). It is different from filter in that it does not filter the light according to the pigment color. It instead allows all the light to pass through unchanged. It can be specified like this: rgbt <1,0,0,1>.
Let's use some transparent pigments to create another kind of texture, the layered texture. Returning to our previous example, declare the following texture.
#declare LandArea = texture {
pigment {
agate
turbulence 1
lambda 1.5
omega .8
octaves 8
color_map {
[0.00 color rgb <.5, .25, .15>]
[0.33 color rgb <.1, .5, .4>]
[0.86 color rgb <.6, .3, .1>]
[1.00 color rgb <.5, .25, .15>]
}
}
}
This texture will be the land area. Now let's make the oceans by declaring the following.
#declare OceanArea = texture {
pigment {
bozo
turbulence .5
lambda 2
color_map {
[0.00, 0.33 color rgb <0, 0, 1>
color rgb <0, 0, 1>]
[0.33, 0.66 color rgbf <1, 1, 1, 1>
color rgbf <1, 1, 1, 1>]
[0.66, 1.00 color rgb <0, 0, 1>
color rgb <0, 0, 1>]
}
}
}
Note: Now the ocean is the opaque blue area and the land is the clear area which will allow the underlying texture to show through.
Now, let's declare one more texture to simulate an atmosphere with swirling clouds.
#declare CloudArea = texture {
pigment {
agate
turbulence 1
lambda 2
frequency 2
color_map {
[0.0 color rgbf <1, 1, 1, 1>]
[0.5 color rgbf <1, 1, 1, .35>]
[1.0 color rgbf <1, 1, 1, 1>]
}
}
}
Now apply all of these to our sphere.
sphere {
<0,0,0>, 1
texture { LandArea }
texture { OceanArea }
texture { CloudArea }
}
We render this and have a pretty good rendition of a little planetoid. But it could be better. We do not particularly like the appearance of the clouds. There is a way they could be done that would be much more realistic.
Using Pigment Maps
Pigments may be blended together in the same way as the colors in a color
map using the same pattern keywords and a pigment_map. Let's
just give it a try.
We add the following declarations, making sure they appear before the other declarations in the file.
#declare Clouds1 = pigment {
bozo
turbulence 1
color_map {
[0.0 color White filter 1]
[0.5 color White]
[1.0 color White filter 1]
}
}
#declare Clouds2 = pigment {
agate
turbulence 1
color_map {
[0.0 color White filter 1]
[0.5 color White]
[1.0 color White filter 1]
}
}
#declare Clouds3 = pigment {
marble
turbulence 1
color_map {
[0.0 color White filter 1]
[0.5 color White]
[1.0 color White filter 1]
}
}
#declare Clouds4 = pigment {
granite
turbulence 1
color_map {
[0.0 color White filter 1]
[0.5 color White]
[1.0 color White filter 1]
}
}
Now we use these declared pigments in our cloud layer on our planetoid. We replace the declared cloud layer with.
#declare CloudArea = texture {
pigment {
gradient y
pigment_map {
[0.00 Clouds1]
[0.25 Clouds2]
[0.50 Clouds3]
[0.75 Clouds4]
[1.00 Clouds1]
}
}
}
We render this and see a remarkable pattern that looks very much like weather patterns on the planet earth. They are separated into bands, simulating the different weather types found at different latitudes.
Normals
Objects in POV-Ray have very smooth surfaces. This is not very realistic so there are several ways to disturb the smoothness of an object by perturbing the surface normal. The surface normal is the vector that is perpendicular to the angle of the surface. By changing this normal the surface can be made to appear bumpy, wrinkled or any of the many patterns available. Let's try a couple of them.
Using Basic Normal Modifiers
We comment out the planetoid sphere for now and, at the bottom of the file, create a new sphere with a simple, single color texture.
sphere {
<0,0,0>, 1
pigment { Gray75 }
normal { bumps 1 scale .2 }
}
Here we have added a normal block in addition to the
pigment block (note that these do not have to be included in a
texture block unless they need to be transformed together or need to
be part of a layered texture). We render this to see what it looks like. Now,
one at a time, we substitute for the keyword bumps the following
keywords: dents, wrinkles,
ripples and waves
(we can also use any of the patterns listed in Pattern).
We render each to see what they look like. We play around with the float value that follows the
keyword. We also experiment with the scale value.
For added interest, we change the plane texture to a single color with a normal as follows.
plane {
y, -1.5
pigment { color rgb <.65, .45, .35> }
normal { dents .75 scale .25 }
}
Blending Normals
Normals can be layered similar to pigments but the results can be unexpected. Let's try that now by editing the sphere as follows.
sphere {
<0,0,0>, 1
pigment { Gray75 }
normal { radial frequency 10 }
normal { gradient y scale .2 }
}
As we can see, the resulting pattern is neither a radial nor a gradient. It is instead the result of first calculating a radial pattern and then calculating a gradient pattern. The results are simply additive. This can be difficult to control so POV-Ray gives the user other ways to blend normals.
One way is to use normal maps. A normal map works the same way as the pigment map we used earlier. Let's change our sphere texture as follows.
sphere {
<0,0,0>, 1
pigment { Gray75 }
normal {
gradient y
frequency 3
turbulence .5
normal_map {
[0.00 granite]
[0.25 spotted turbulence .35]
[0.50 marble turbulence .5]
[0.75 bozo turbulence .25]
[1.00 granite]
}
}
}
Rendering this we see that the sphere now has a very irregular bumpy surface. The gradient pattern type separates the normals into bands but they are turbulated, giving the surface a chaotic appearance. But this gives us an idea.
Suppose we use the same pattern for a normal map that we used to create the oceans on our planetoid and applied it to the land areas. Does it follow that if we use the same pattern and modifiers on a sphere the same size that the shape of the pattern would be the same? Would not that make the land areas bumpy while leaving the oceans smooth? Let's try it. First, let's render the two spheres side-by-side so we can see if the pattern is indeed the same. We un-comment the planetoid sphere and make the following changes.
sphere {
<0,0,0>, 1
texture { LandArea }
texture { OceanArea }
//texture { CloudArea } // <-comment this out
translate -x // <- add this transformation
}
Now we change the gray sphere as follows.
sphere {
<0,0,0>, 1
pigment { Gray75 }
normal {
bozo
turbulence .5
lambda 2
normal_map {
[0.4 dents .15 scale .01]
[0.6 agate turbulence 1]
[1.0 dents .15 scale .01]
}
}
translate x // <- add this transformation
}
We render this to see if the pattern is the same. We see that indeed it
is. So let's comment out the gray sphere and add the normal
block it contains to the land area texture of our planetoid. We remove the
transformations so that the planetoid is centered in the scene again.
#declare LandArea = texture {
pigment {
agate
turbulence 1
lambda 1.5
omega .8
octaves 8
color_map {
[0.00 color rgb <.5, .25, .15>]
[0.33 color rgb <.1, .5, .4>]
[0.86 color rgb <.6, .3, .1>]
[1.00 color rgb <.5, .25, .15>]
}
}
normal {
bozo
turbulence .5
lambda 2
normal_map {
[0.4 dents .15 scale .01]
[0.6 agate turbulence 1]
[1.0 dents .15 scale .01]
}
}
}
Looking at the resulting image we see that indeed our idea works! The land areas are bumpy while the oceans are smooth. We add the cloud layer back in and our planetoid is complete.
There is much more that we did not cover here due to space constraints. On our own, we should take the time to explore slope maps, average and bump maps.
Slope Map Tutorial
One of the most powerful texturing features of POV-Ray is normal perturbation (which is specified using the normal block of an object texture). With this feature it's possible to emulate small surface displacement in a very efficient way, without actually having to modify the actual surface (which often would increase the complexity of the object considerably, resulting in much slower renders).
Slope maps are used to define more precisely how the normal perturbation is generated from a specified pattern. Slope maps are a very powerful feature often dismissed by many.
As an example, let's create a simple scene with an object using normal perturbation:
camera { location <0, 10, -7>*1.4 look_at 0 angle 35 }
light_source
{ <100, 80, -30>, 1 area_light z*20, y*20, 12, 12 adaptive 0 }
plane { y, 0 pigment { rgb 1 } }
cylinder
{ 0, y, 4
pigment { rgb <1, .9, .2> }
finish { specular 1 }
normal
{ wood 1
rotate x*90
}
}
|
Normal modifier example |
By default the wood pattern uses a ramp wave (going from 0 to 1 and then back to 0) arranged in concentric circles, as we can see from the image.
By default POV-Ray simply takes the values of the pattern as they are in order to calculate the normal perturbation of the surface. However, using a slope_map we can more precisely define how these values are interpreted. For example, if we add this slope_map (the meaning of the values are explained later in this tutorial) to the normal block in the example above:
slope_map
{ [0 <0, 0>]
[.2 <1, 1>]
[.2 <1, 0>]
[.8 <1, 0>]
[.8 <1, -1>]
[1 <0, 0>]
}
we get a much more interesting result:
|
Slope map example 1 |
We can also use a slope map to simply smooth out the original ramp wave pattern like this:
slope_map
{ [0 <0, 0>]
[.5 <.5, 1>]
[1 <1, 0>]
}
|
Slope map example 2 |
Slopes, what are they?
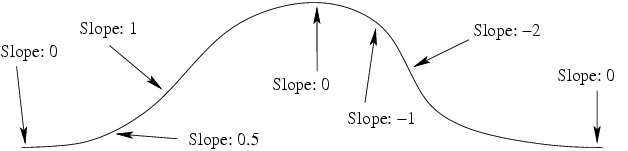
Mathematically speaking the slope of a curve (also called gradient) at a certain point is the tan() of the angle of the tangent line of that curve at that point. In other words, it's the amount of change of the vertical coordinate with respect to the change of the horizontal coordinate.
In a more colloquial way, the slope of a completely horizontal part of the curve is 0. The slope of a 45-degree line is 1 (because for each unit in the horizontal direction the line goes up by the same amount). Lines between 0 and 45 degrees have corresponding slopes between 0 and 1 (the relation between them is not linear, though, but one usually doesn't have to worry about that). Lines with an angle of over 45 degrees have correspondently slopes increasingly larger than 1 (a line of 90 degrees has an infinite slope).
Usually when defining slope maps it's enough to keep between slopes of 0 and 1, even though higher slopes are sometimes useful too to get steeper changes. Usually it's enough to think that a slope of 0 means a horizontal part of the curve while a slope of 1 means a 45-degree steep part of the curve (and slopes between 0 and 1 correspond to degrees between 0 and 45 respectively).
A slope can be negative too. A negative slope simply means that the curve is going down instead of going up.
The following figure shows some basic slopes in a curve (note that the slope values are only approximate):
|
Slopes in a curve |
Syntax of a slope map
In the exact same way as for example a color_map assigns colors to pattern values, a slope_map assign slopes to pattern values. If you are fluent in defining color maps for a pattern, defining a slope map shouldn't be any more difficult.
Each entry in a slope map takes two values: The displacement of the surface (although one should remember that this displacement is only simulated, not real) and the slope of the surface at that point.
You can think of the first parameter as an altitude value which tells how much the surface (in relative terms) is displaced from its original location. Usually values between 0 and 1 are used for this. You can think of 0 meaning that the surface is not displaced and 1 as the surface having maximum displacement (outwards).
Let's examine the slope map we used to smooth out the wood pattern at the beginning of this tutorial:
slope_map
{ [0 <0, 0>]
[.5 <.5, 1>]
[1 <1, 0>]
}
This means:
- When the pattern has a value of 0, the surface is not displaced and the slope of the surface is 0 (ie. it's horizontal).
- When the pattern has a value of 0.5, the surface is displaced by 0.5 and the slope of the surface is 1.
- When the pattern has a value of 1, the surface has maximum displacement and the slope is again 0, ie. horizontal.
When the pattern is linear (as the wood pattern is), this kind of slope map corresponds approximately to a half sine wave. Since the wood pattern uses a ramp wave (ie. after going from 0 to 1 it then goes from 1 to 0), the result is basically a complete (approximate) sine wave.
As with a color map, all the values in between are interpolated and that's why we get a smooth transition between these values.
Examples of slope maps
As we saw in the first slope map example in this tutorial, it is possible to create sharp transitions, not just smooth ones. This is achieved in the same way as how sharp transitions are achieved with color maps: By repeating the same pattern value. Here is an example:
slope_map
{ [0 <0, 1>]
[.5 <1, 1>]
[.5 <1, -.3>]
[1 <.7, -.3>]
}
|
Slope map example 3 |
There's a sharp transition at the pattern value 0.5, where the surface goes from slope 1 to slope -0.3 (ie. from going strongly upwards to going slightly downwards). Due to how the wood pattern repeats itself, there are also sharp transitions at the pattern values 0 and 1.
We can combine sharp and smooth transitions for nice effects. For example, this simple slope map achieves a nice result:
slope_map
{ [0 <0, 1>]
[1 <1, 0>]
}
|
Slope map example 4 |
- At the pattern value 0 the displacement of the surface is 0 and the slope is 1 (ie. strongly upwards).
- At the pattern value 1 the surface is fully displaced and horizontal.
- Due to the ramp-wave-repetition quality of the wood pattern (which effectively reverses this pattern), the surface then continues smoothly from this point until it descends to 0, where the slope is now effectively -1. Now there's a sharp transition from -1 back to 1 as the pattern starts over.
One application where slope maps are really useful is when creating tiled floors. When the tiles on a floor are not too close to the camera and there is a very large amount of tiles, instead of creating hundreds or thousands of individual tile objects, it may be more efficient to simply create a normal pattern which emulates the tiles.
This example shows how to create a floor made of wooden planks:
camera { location <2, 10, -12>*.5 look_at 0 angle 35 }
light_source
{ <100, 150, 0>, 1 area_light z*40, y*40, 12, 12 adaptive 0 }
sphere { y*.5, .5 pigment { rgb x } finish { specular .5 } }
plane
{ y, 0
pigment
{ wood color_map { [0 rgb <.9,.7,.3>][1 rgb <.8,.5,.2>] }
turbulence .5
scale <1, 1, 20>*.2
}
finish { specular 1 }
normal
{ gradient x 1
slope_map
{ [0 <0, 1>] // 0 height, strong slope up
[.05 <1, 0>] // maximum height, horizontal
[.95 <1, 0>] // maximum height, horizontal
[1 <0, -1>] // 0 height, strong slope down
}
}
}
|
Slope map example 5 |
In this case a gradient pattern was used. Since the gradient pattern goes from 0 to 1 and then immediately back to 0, we have to mirror the slope map (around 0.5) in order to get a repetitive symmetric result.
In this example the slope map starts from 0 height and a strong slope up, and goes quickly to maximum height, where the surface is horizontal. Then there's a large horizontal area (from pattern value 0.5 to 0.95) after which the slope goes rapidly back down to 0 height and a strong slope down. (After this there's a sharp transition to the beginning due to the gradient pattern starting over.)
If we want square tiles instead of just planks, we can achieve that by eg. using an average normal map like this:
#declare TileNormal =
normal
{ gradient x 2 // Double the strength because of the averaging
slope_map
{ [0 <0, 1>] // 0 height, strong slope up
[.05 <1, 0>] // maximum height, horizontal
[.95 <1, 0>] // maximum height, horizontal
[1 <0, -1>] // 0 height, strong slope down
}
}
normal
{ average normal_map
{ [1 TileNormal]
[1 TileNormal rotate y*90]
}
}
|
Slope map example 6 |
If we change the pigment of the plane a bit, we get a nice tiled floor:
pigment
{ checker
pigment { granite color_map { [0 rgb 1][1 rgb .9] } }
pigment { granite color_map { [0 rgb .9][1 rgb .7] } }
}
|
Slope map example 7 |
As you can see in the image, close to the camera it's more evident that the tiles are not truely three-dimensional (and that only a normal perturbation trick has been used), but farther away from the camera the effect is pretty convincing.
Finishes
The final part of a POV-Ray texture is the finish. It
controls the properties of the surface of an object. It can make it shiny and
reflective, or dull and flat. It can also specify what happens to light that
passes through transparent pigments, what happens to light that is scattered
by less-than-perfectly-smooth surfaces and what happens to light that is
reflected by surfaces with thin-film interference properties. There are
twelve different properties available in POV-Ray to specify the finish of a
given object. These are controlled by the following keywords: ambient,
diffuse, brilliance,
phong, specular, metallic, reflection, crand and iridescence. Let's design a couple of textures that make use of these parameters.
Using Ambient
Since objects in POV-Ray are illuminated by light sources, the portions of
those objects that are in shadow would be completely black were it not for
the first two finish properties, ambient and
>diffuse. Ambient is used to simulate the light that is scattered
around the scene that does not come directly from a light source. Diffuse
determines how much of the light that is seen comes directly from a light
source. These two keywords work together to control the simulation of ambient
light. Let's use our gray sphere to demonstrate this. Let's also
change our plane back to its original green and white checkered pattern.
plane {
y, -1.5
pigment {checker Green, White}
}
sphere {
<0,0,0>, 1
pigment { Gray75 }
finish {
ambient .2
diffuse .6
}
}
In the above example, the default values for ambient and diffuse are used. We render this to see what the effect is and then make the following change to the finish.
ambient 0 diffuse 0
The sphere is black because we have specified that none of the light
coming from any light source will be reflected by the sphere. Let's
change diffuse back to the default of 0.6.
Now we see the gray surface color where the light from the light source
falls directly on the sphere but the shaded side is still absolutely black.
Now let's change diffuse to 0.3 and ambient to
0.3.
The sphere now looks almost flat. This is because we have specified a fairly
high degree of ambient light and only a low amount of the light coming from
the light source is diffusely reflected towards the camera. The default
values of ambient and diffuse are pretty good
averages and a good starting point. In most cases, an ambient value of 0.1
... 0.2 is sufficient and a diffuse value of 0.5 ... 0.7 will usually do the
job. There are a couple of exceptions. If we have a completely transparent
surface with high refractive and/or reflective values, low values of both
ambient and diffuse may be best. Here is an example:
sphere {
<0,0,0>, 1
pigment { White filter 1 }
finish {
ambient 0
diffuse 0
reflection .25
specular 1
roughness .001
}
interior { ior 1.33 }
}
This is glass, obviously. Glass is a material that takes nearly all of its
appearance from its surroundings. Very little of the surface is seen because
it transmits or reflects practically all of the light that shines on it. See
glass.inc for some other examples.
Note: As of POV-Ray v3.7, ambient is disabled when using radiosity, as both mechanisms are intended to simulate the same thing (albeit with different quality) and don't play well together.
Using Emission
If we ever need an object to be completely illuminated independently of the
lighting situation in a given scene we can do this artificially by specifying
an emission value of 1 and an ambient and diffuse value of 0.
This will eliminate all shading and simply give the object its fullest and
brightest color value at all points. This is good for simulating objects that
emit light like light bulbs and for skies in scenes where the sky may not be
adequately lit by any other means.
Let's try this with our sphere now.
sphere {
<0,0,0>, 1
pigment { White }
finish {
emission 1
ambient 0
diffuse 0
}
}
Rendering this we get a blinding white sphere with no visible highlights or shaded parts. It would make a pretty good street light.
Note: Versions of POV-Ray prior to 3.7 did not provide the emission keyword for finish, and it was customary to resort to ambient instead for such purpose. This is now discouraged, as ambient is now disabled when using radiosity.
| Polynomial made easy | Using Surface Highlights |
|
This document is protected, so submissions, corrections and discussions should be held on this documents talk page. |